A Different Kind Of Tree

How It Works

Instead of being a binary tree, the Two Three tree has nodes that can hold two data values and that have three reference links to nodes below*. The interesting thing about the Two Three tree is that the bottom is always flat; in other words, the bottom row of leaves are all at the same level. When new nodes must be added, they are added at the top of the tree as shown here where the value 90 is added to the tree.

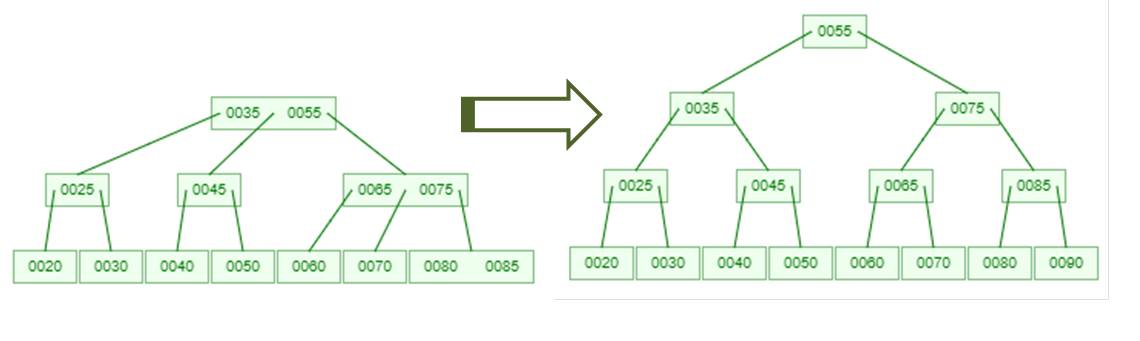
Image Credit: Screenshot from USFCA animation, David Galles, Curator

As mentioned the bottom of the tree is always flat (i.e., the lowest leaves will all be at the same level in the tree) and the tree is always fully balanced thanks to the strategy of adding a new node above the current nodes when the rest of the tree cannot appropriately hold the new data. The Two Three tree can actually be related to a Red Black tree so it is a little more complicated than the other self balancing trees but as mentioned previously, complicated just means you handle small parts of the process one at a time and from there you can get the whole thing programmed. Complicated does not mean difficult.

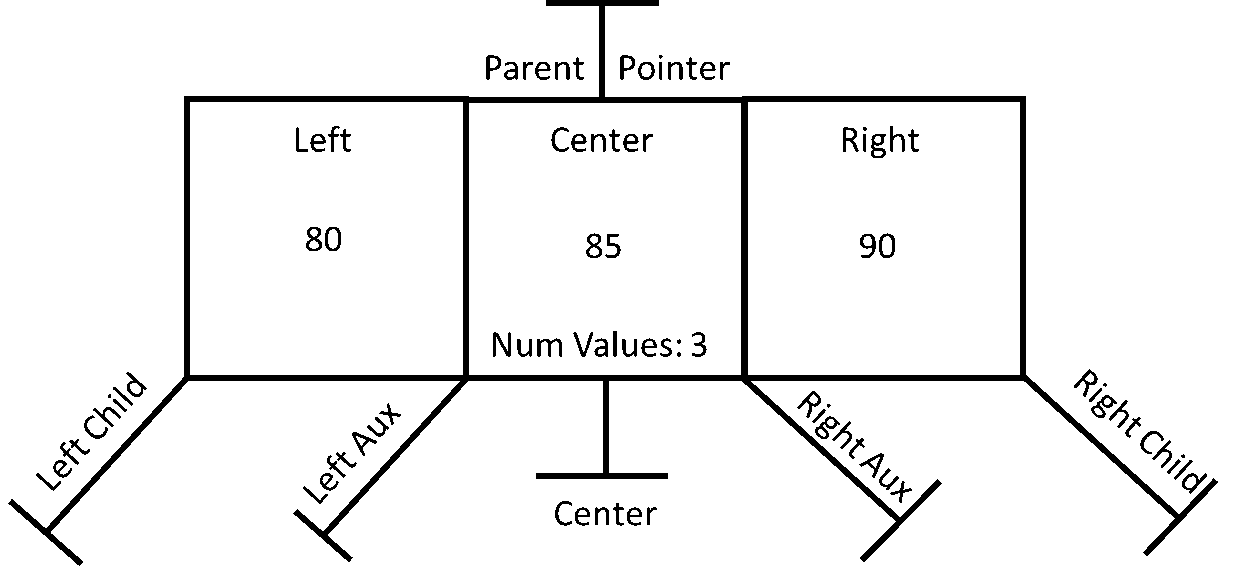
*With the introductory discussion provided, there needs to be a little explanation here. The nodes are actually capable of holding one more data item and one more reference link than specified. For example, the Two Three nodes can actually hold three data items and link to four nodes below. However, this is only allowed during a transition, not when the tree is in its normal static state.

Watch How This Works

The two-three node actually starts out life as a three-four node; that is, it will have three data items and four child pointers. When the tree is balanced and not in transition, only parts of the node will be used. For example, if there is a one data node, only the center value and outer left and right pointers are used. If there is a two data node, only the left and right data values are used (not the center), and the left, center, and right child pointers are used. These two conditions are appropriate for a two three tree. However, during a transition, all three values and all four pointers are used. You will see this operation soon. That said, it must be noted that there are other ways to handle managing transitions. This strategy is used for its clarity. Consider the following empty node.

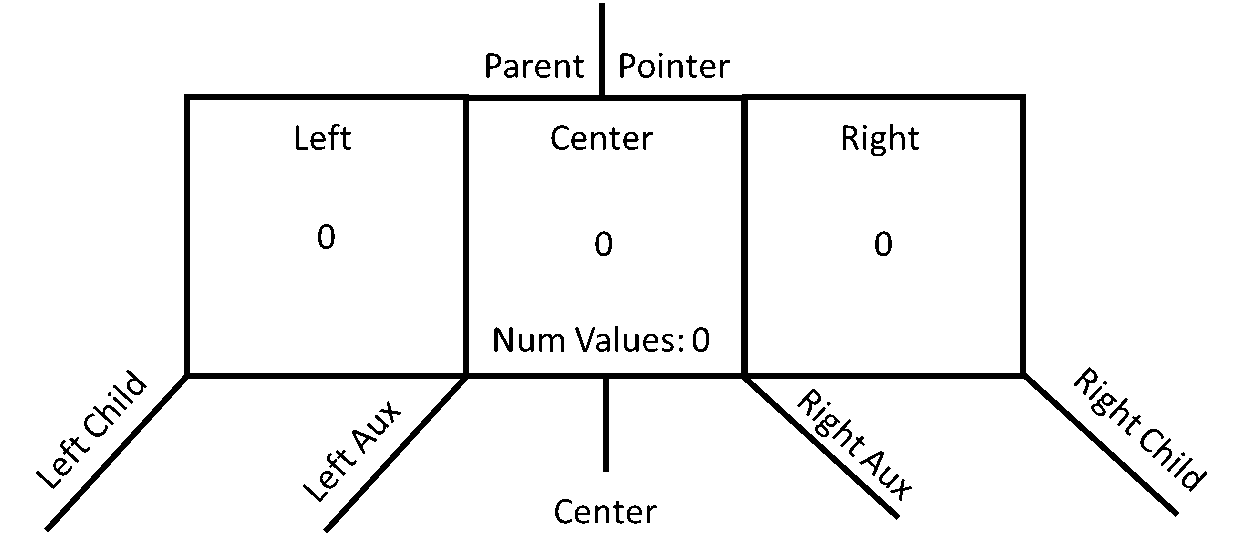
A default node would actually start out showing a number of values of one since that is the only choice when it first gets its data, but this is shown as zero to indicate the concept. And while it is not shown to save space, all four child pointers would be set to NULL.

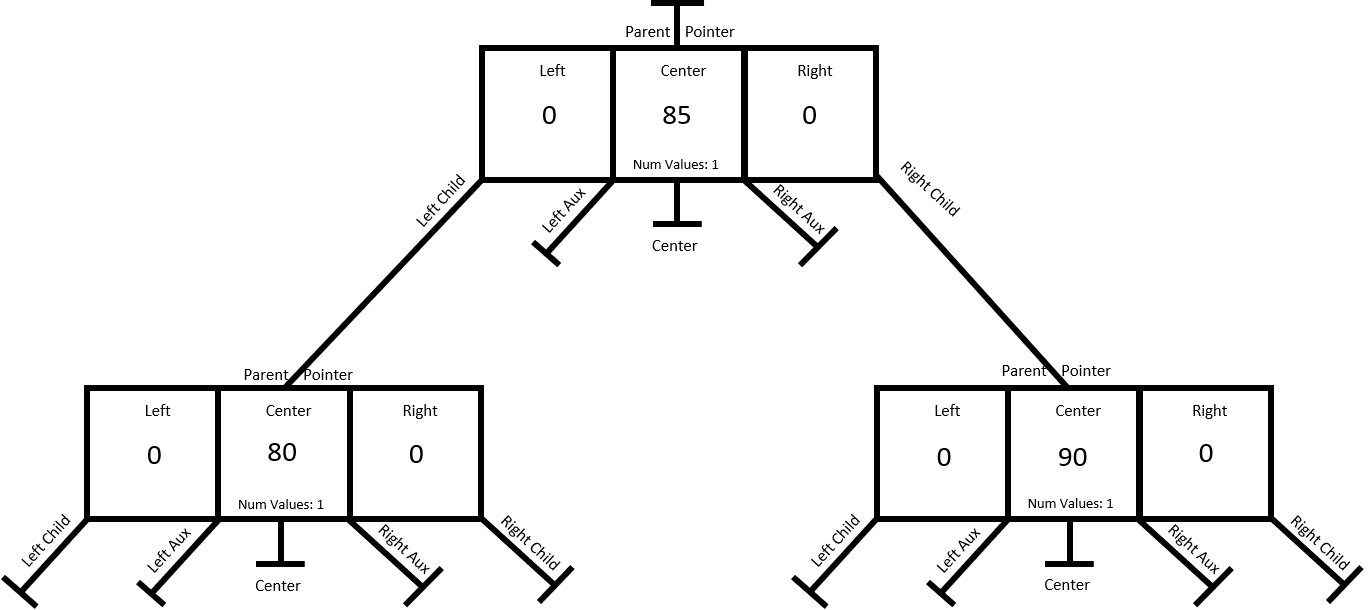
Like most other trees, there will never actually be an empty node. When the very first node is added to the tree, the node is created and the center value is set, as shown here.

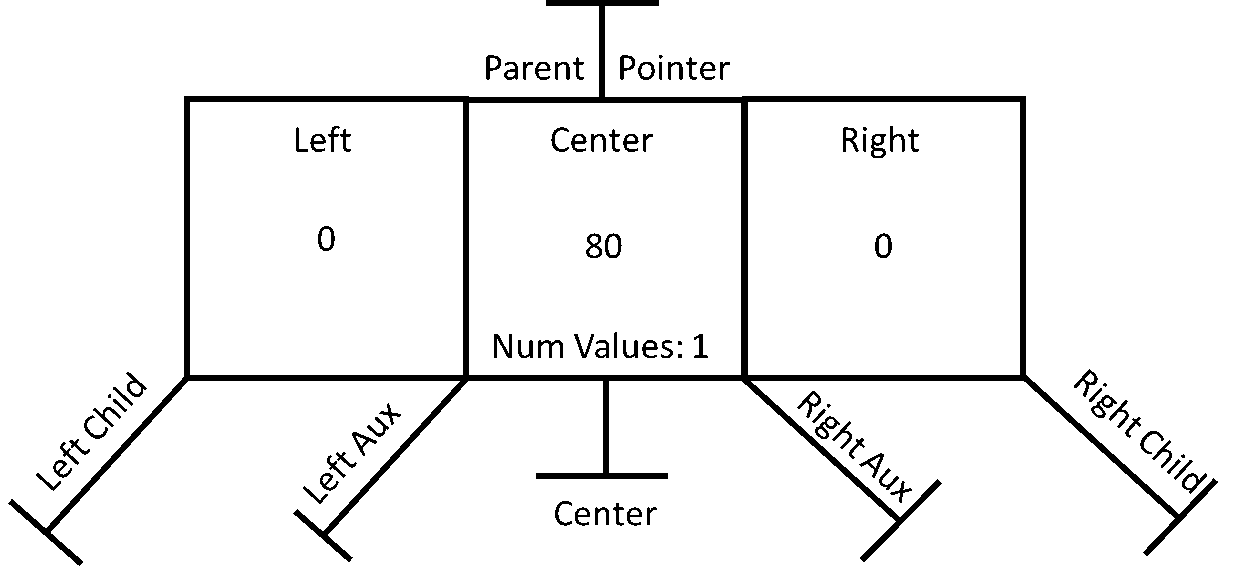
This is showing how a node would work when it is the first one added to the tree. The parent pointer would be set to NULL as would all the children. For one thing, this makes the node a leaf or leaf node, and even though the parent pointer of the root node is NULL, the tree root pointer of the 2-3 tree is set to point at this node.

Next up is what the node would look like if the value 85 was added. Remember that the worst condition for a tree is to have data entered that is already in order. Unbalanced trees would suffer from this, but this tree will handle it. Check it out.

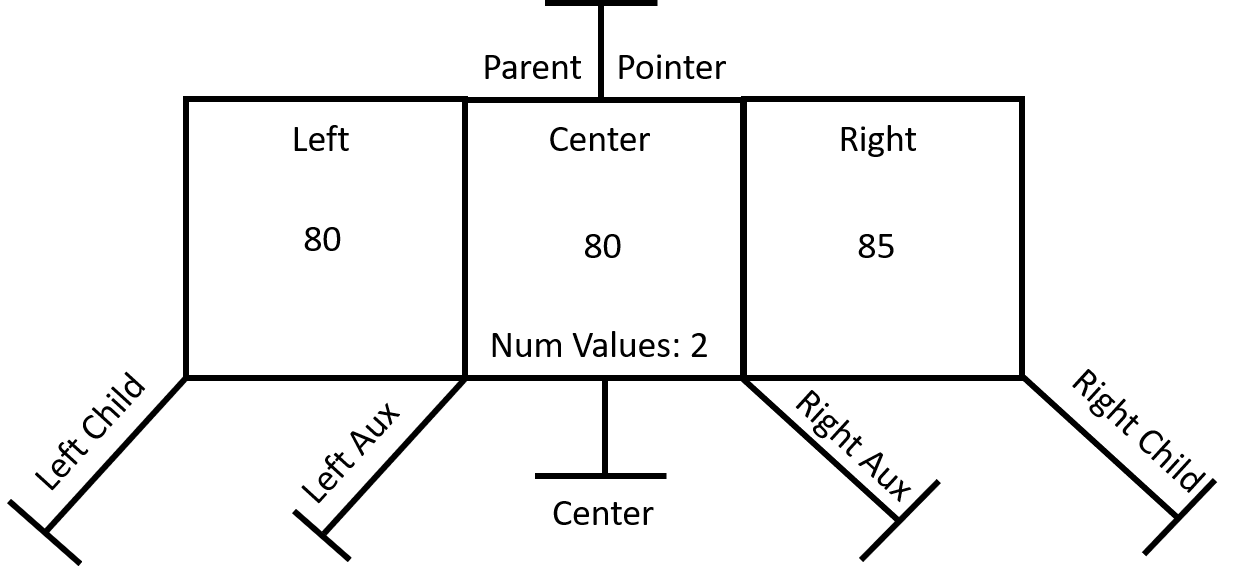
When the code gets to the place where it is adding the value -- which is called "add and organize" -- it will check to see where the value goes and place it appropriately. In this case, it will place the value on the right side, and the other value on the left side. As you can see, the original value is still in the center but this will never be accessed when the number of values is set to two. To repeat from above, when the number of values is set to one, only the center value is accessed; when the number of values is set to two, only the left and right values are accessed. This is built into the code.

Now a reminder here that this could be the first node created in this tree. However, it doesn't have to be. It could be the 97th item and it would still do the same thing. In all cases, the tree is searched all the way to the bottom (i.e., a leaf node) for the appropriate node, and then the data is added. And at this point, for this node, all is good.

However . . . What happens if another value is added that lands in this leaf node? Take a look here.

Once again, the add and organize data process kicks in when the search gets to the appropriate bottom or leaf node, and it will make a three-four node out of the data and the previous two-three node. Now as you recall, this is not a legal node in a two-three tree but it is acceptable during an add/transition process, and here it is.

The other function called after the add and organize data function is called the fix up function. The fix up function only works on three-four nodes so up to this point, it has not taken any action. However, when it recognizes the three-four node, it splits the node up into three parts, as shown here.

As you can see, the bottom stays flat. In other words, the lowest level of nodes will all be at the same height or distance from the root node. However, the new node was created above the other two so the tree will naturally always be balanced. Note also that each of the three nodes is back to being a one-two node with a single data item but you can now recognize that the upper node has pointers to the two lower nodes.

To expand on that, when a second value is added to a node that is not a leaf node, it will use the left, center, and right child pointers in addition to placing the left and right data values. Finally, when a third value is added to a non-leaf node, it will place all three data items in the right order and use the left and left aux pointers and the right and right aux pointers.

Then when a non-leaf node is split up into three nodes -- exactly the same way the above one was split, the left/left aux pointers become the left/right pointers for the node created to the left and the right aux/right pointers become the left/right pointers for the node created to the right.

And yes, it does get complicated when setting all the nodes, including having to set the parent nodes for each of these, but you just draw your pictures and make the links one at a time in your code, and that takes care of it.

Consider the following "before" state shown in the first graphic above. This only shows the bottom right nodes.

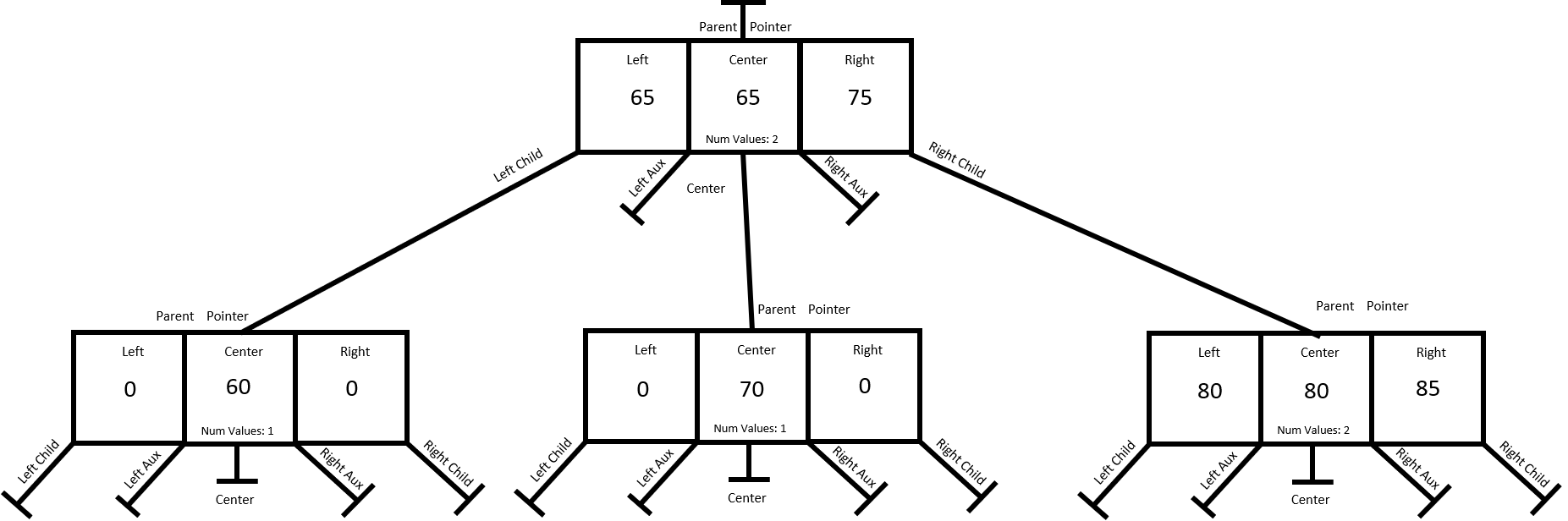
The bottom nodes are a one node, one node, two node at this point. The parent node is a two node. For the two nodes, the center does not matter since it is not accessed in a two node. Now, what happens when you add the values 90 to this tree. The value will work its way down to the bottom leaf node, which is the lower right node. The add and organize data process will set the 90 value in what is now a three node, which will look like the following

At this point, the lower right node is now a three node, so when the fix up is called with the pointer to this node, the fix up process goes into action.

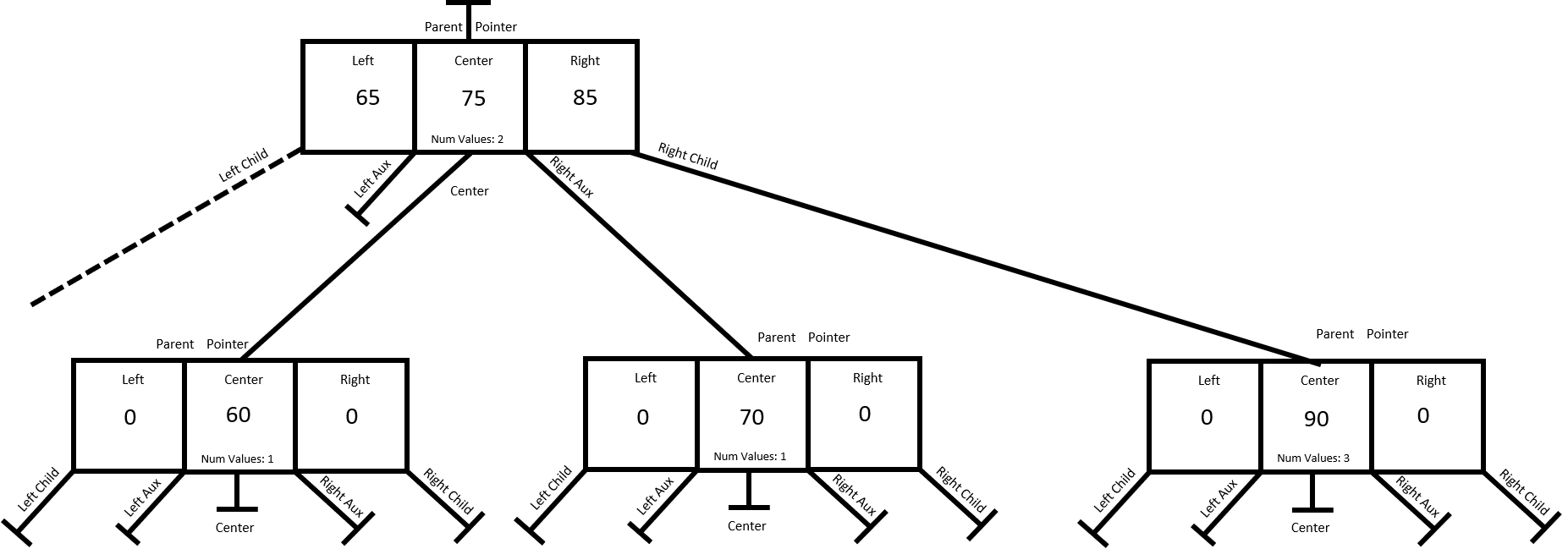
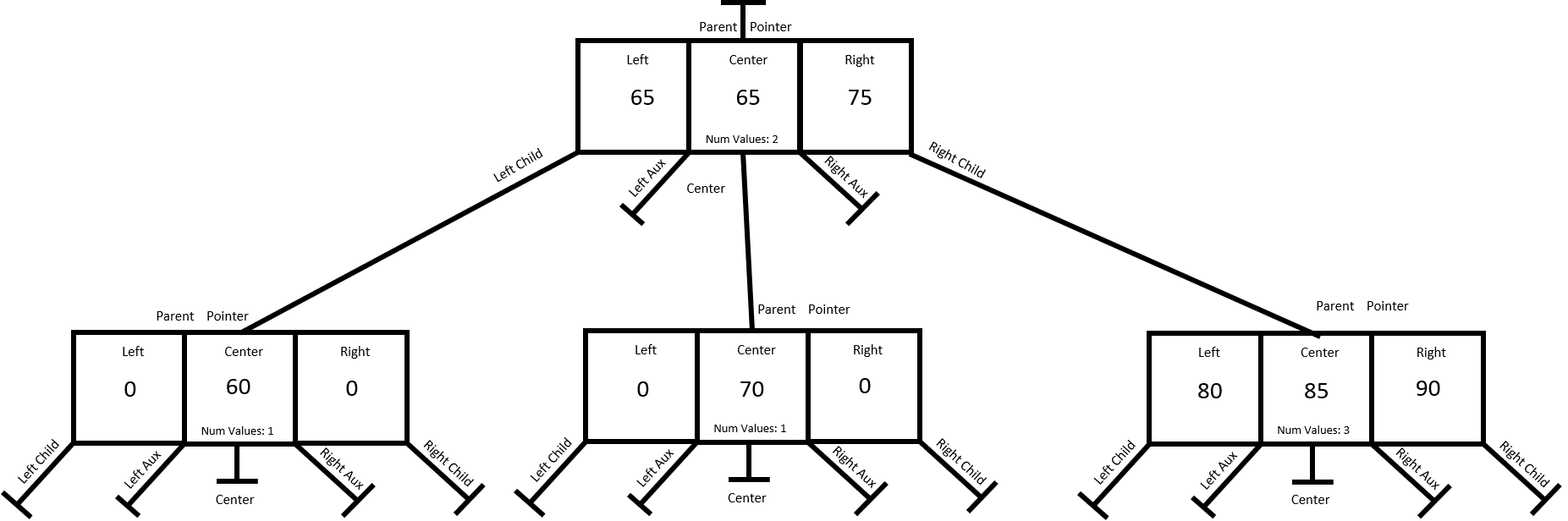
To save some space and make the graphic usable, the far left node is not shown. For this circumstance, that node would not be modified. Only the center and right nodes are affected. As you can see the three node leaf has been broken into two nodes below and the 85 has been raised up into the right side of the parent node, which you should see, is now a three node.

When the fix up process has completed at a given level, it will recursively call itself at the parent level which, as you can also see, is now a three node and would be broken up into two parts while moving the center value up to the next parent node. The final result (from above) is shown here.

Image Credit: Screenshot from USFCA animation, David Galles, Curator

Once again, the bottom, or leaf nodes, always stay at the same level which makes the bottom of the three "flat". This is as balanced as a tree can be.

One More Note about Searching

In one sense, there are a lot of moving parts here. In another sense, you have seen it all in this topic. The tree is manipulated the same way every time. The one thing remaining to consider is how to search a tree like this, and the answer is not difficult.

Like all trees, the search starts at the tree root and makes its decisions one node at a time. At any node, the first test is to see if the current node is NULL; if that is the case, the data is not in the tree and NULL is returned. The second test is to see if the value has been found; this involves calling a function that simply looks at the center value for a one node or the left and right values for a two node and reports if they are the desired value. If the value has not been found and the current node is a one node, then the decision will be made to go either left or right. Otherwise, assuming it is a two node, the value will go to the left child of the left value, the right child of the right value, or the center child if the value is between the left and right values. And to be clear, the code is simpler than this discussion . . .

Two Three Trees

Two three trees are a really interesting data structure, and obviously quite powerful. The complexity of this tree is still very close to Log₂(N), so millions of data items can be easily and quickly stored and accessed. Removal of data is not discussed in this topic because it really is just a reversal of the add item operation, but it is complicated enough that pursuing the process would be beyond the educational goals of this reference. Next up is the heap data structure, which is still another implemenation of a tree, in an array. It's pretty cool.