Upgrading, In Color

How It Works

The Red-Black tree adds an extra data item to each node that is the color for that node, and it adds a third pointer to the parent of each node in addition to the child pointers. As you might imagine, the colors are red and black. With this small addition, there are six rules that are followed to create a self-balancing tree. The data is added to the tree as a red node in the normal way for BST trees and, after the insertion, the tree is readjusted according to the four rules.

The rules are:

1. Every node will have a color, red or black (we knew that)


2. The root node must always be black


3. Every new node starts out red


4. Any NULL nodes (empty child nodes) are considered to be black


5. Red nodes may not be vertically adjacent anywhere in the tree. This means that any given parent and either of its children may never both be red. Note that both children could be red but if they are, neither the parent nor the children's children may be red


6. The number of black nodes must always be the same when counting from any given node to the bottom of the tree along any branching path

There are a series of operations that support compliance with these rules but they are pretty simple to follow in a recipe- or algorithm- like operation. Since the resolution process is called after the insertion process, it does require climbing the tree from where the new node was added so this is why a parent pointer is required.

A Red Black tree will allow a maximum difference in tree height of two, meaning none of the lowest leaves will have a height difference greater than two. Remember that an AVL tree only allows a bottom height difference of one, and the 2-3 tree will always have a flat bottom, meaning it's height difference will be the same across the whole tree.

Before moving on, there is a web page you should be familiar with that handles all kinds of data structures in a graphical way. The web site can be found here. It is very worth your while to look at, and play with, this reference to learn more about most data structures, including this Red-Black tree.

The Process Overview

Here is the initial overview of the process, which incorporates the rules provided earlier in this section.

Every new node is added to a Red Black tree exactly the same way it would be added to any other Binary Search Tree (BST). A Red Black tree is just a BST that happens to have some extra capabilities to help it maintain balance.

The new node will always start out with the red color, and the self-balancing actions begin at the location where the new node was added.

The Cases

From the new node's perspective, there are six conditions, or cases, to consider:

• The new node's uncle is red
• The new node's parent is left of the grandparent and the new node is left of the parent. This is called the Left-Left case
• The new node's parent is left of the grandparent and the new node is right of the parent. This is called the Left-Right case
• The new node's parent is right of the grandparent and the new node is right of the parent. This is called the Right-Right case
• The new node's parent is right of the grandparent and the new node is left of the parent. This is called the Right-Left case
• The current node (in the resolve function call) is the root node

Each of these conditions must be resolved, and that resolution is provided next in a function commonly called fixup, resolve, or something similar.

The Resolution

If the Uncle is red,

• Change the Parent and Uncle to Black
• Change the Grandparent to Red
• Call the resolve function recursively with the Grandparent to resolve color conflicts above it

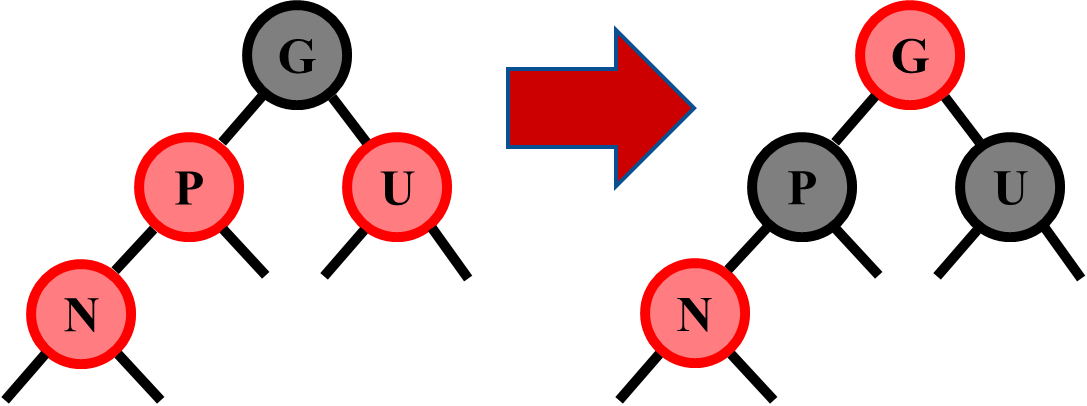
Otherwise, if there is a Left-Left case,

• Rotate (right) Grandparent (old top) to Parent (new top)
• Link Parent to Grandparent's parent
• Swap colors between Parent and Grandparent

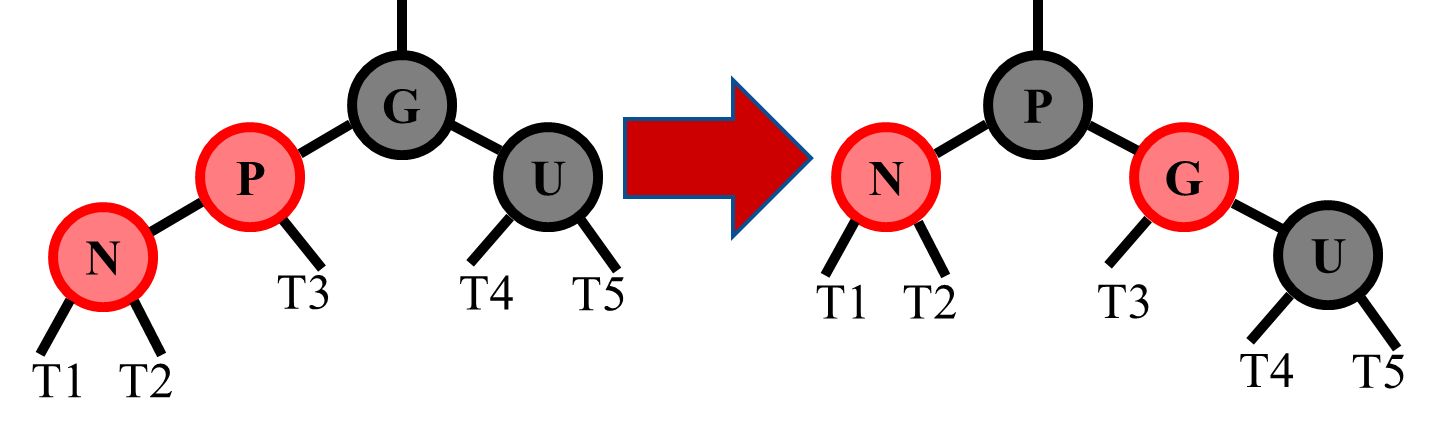
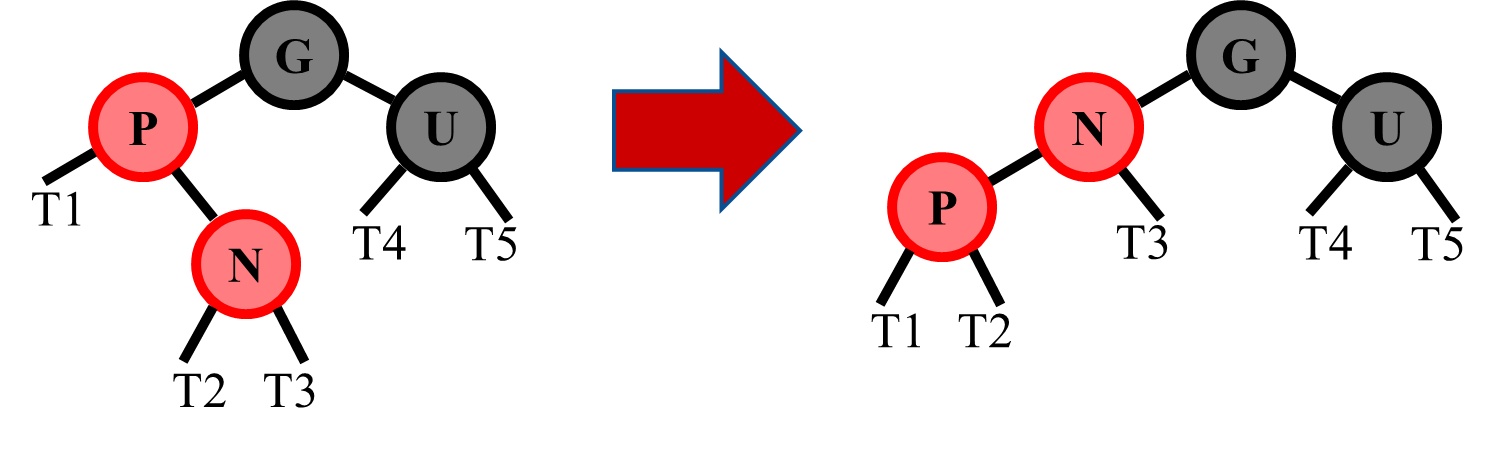
Otherwise, if there is a Left-Right case,

• First, rotate (left) Parent (old top) to Newnode (new top)

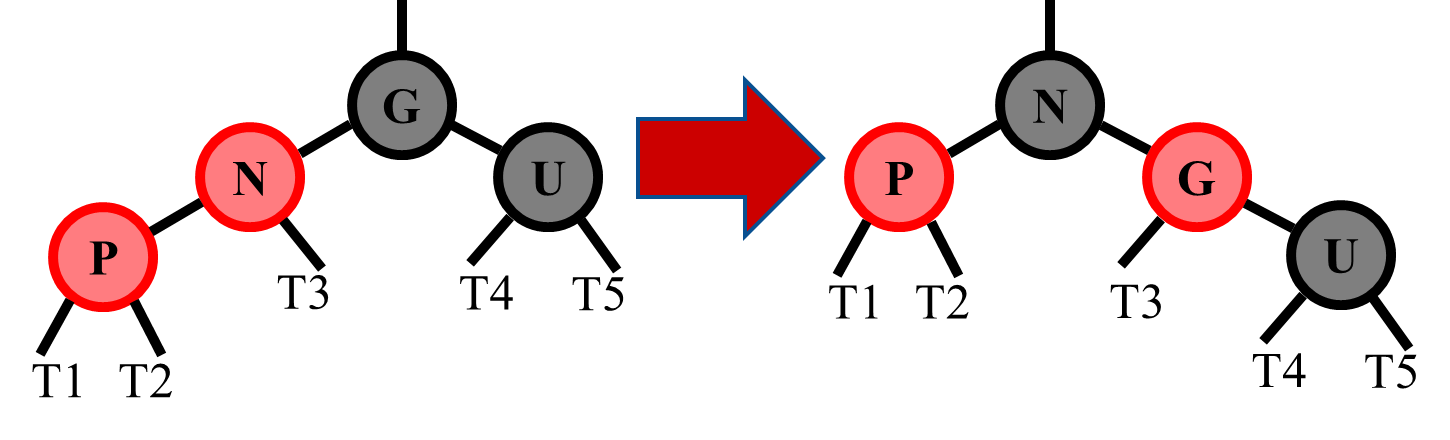
• Then, call resolve function recursively with Parent as Newnode
• Recursion will treat this as a Left-Left case:
• Rotate (right) Grandparent (old top) to Newnode (new top)
• Link Newnode to Grandparent's parent
• Swap colors between Newnode and Grandparent

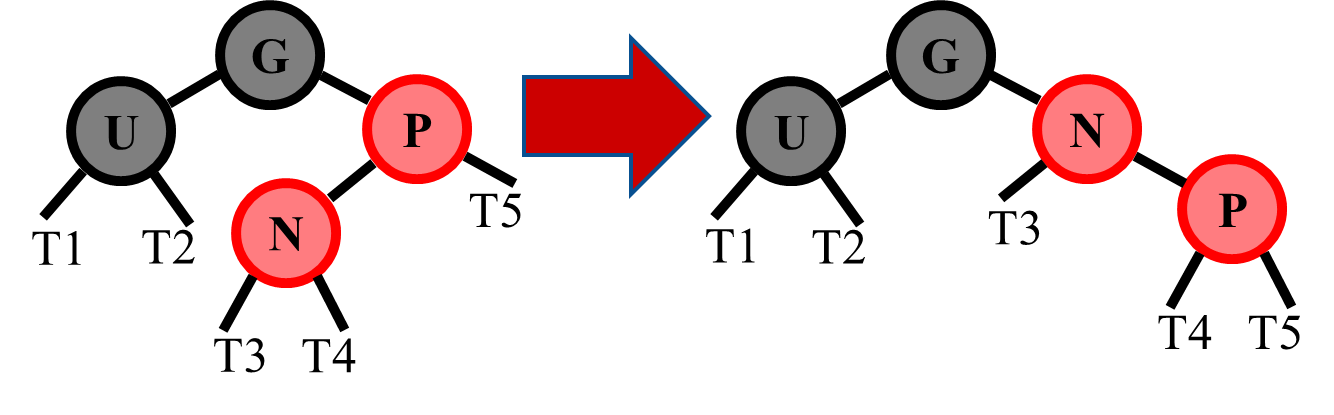
Otherwise, if there is a Right-Right case,

• Rotate (left) Grandparent (old top) to Parent (new top)
• Link Parent to Grandparent's parent
• Swap colors between Parent and Grandparent

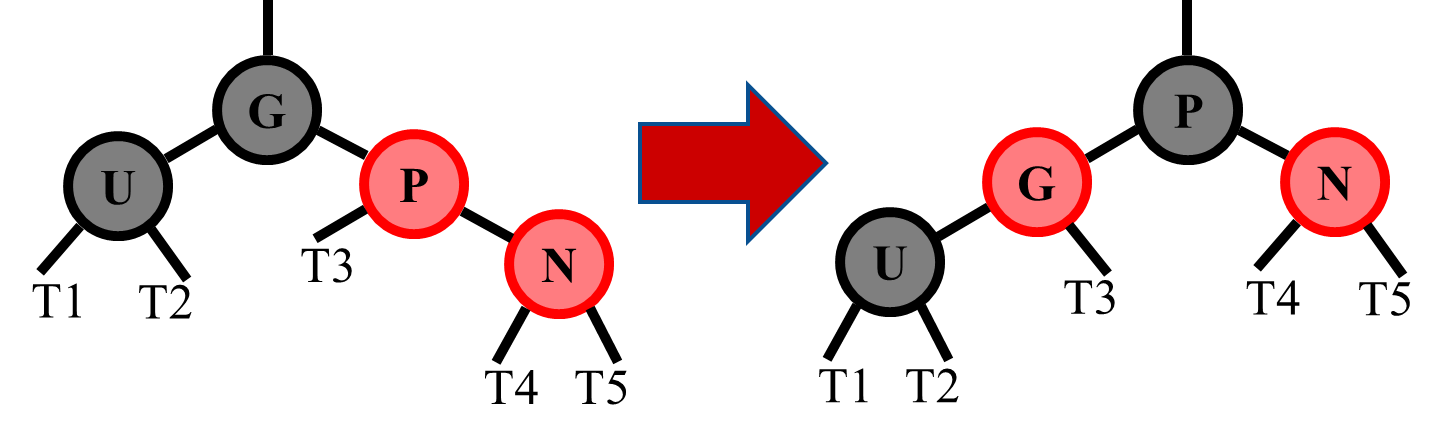
Otherwise, if there is a Right-Left case,

• First, rotate (right) Parent (old top) to Newnode (new top)

• Then, call resolve function with parent as Newnode
• Recursion will treat this as a Right-Right case:
• Rotate (left) Grandparent (old top) to Newnode (new top)
• Link Newnode to Grandparent's parent
• Swap colors between Newnode and Grandparent

Finally, under all conditions,

• Check to see if the current node is the root node; if so, set it to Black
• While only one of the above steps would commonly occur in a given resolve function call, this operation must happen every time, as the last step

And The Rotation?

The rotation occurs exactly like the AVL rotation with the caveat that Red Black Tree rotation also involves a parent pointer. However, there do appear to be two kinds of each rotation. Left rotation can occur with and without involving the grandparent, and so can right rotation.

And while the rotations look a little different, the are functionally identical. The issue is what node to point at going into, and coming out of, the rotation and this is where abstraction really saves the day. When the Parent, Grandparent, or Newnode pointers are called for the rotation, the function should accept the appropriate family members as an old top pointer and a new top pointer. The old/new relationships are provided in the descriptions above, so this should be easy.

When the function itself is written, for example, the rightRotate header would be something like:

   RBT_Node *rotateRight( RBT_Node *oldTop, RBT_Node *newTop )
      {
       // manipulate the code between the old and new tops

       // then return link to new top's parent
      }

The leftRotate header would have the same parameters.

BST With Color

Like other self-balancing trees, Red Black trees make a very powerful data structure -- the BST -- even more powerful by guaranteeing constant Log₂(N) access under every data entry condition. As mentioned above, a Red Black tree will allow a height difference of two at the bottom of the tree, this is negligable relative to any substantial tree. And while the above management can look complicated and potentially intimidating, all that needs to happen is that each case/condition be treated one at a time. And that makes the very powerful pretty easy.