A Tree, In An Array?

First, Some Background

To this point, you have been studying arrays, then linked lists, and then trees. You have discovered that trees can be searched significantly faster than linear lists such as arrays and linked lists and you have had a chance to manage and manipulate several of these data structures to see how they work. The heap is something of a unique data structure in that it is managed like a tree but the data is stored in an array. The good news is that this can get you the best of two worlds, with tree like speed, and with array-like immediate index access. The rest of the story is that a heap is not like a normal data structure in that while you can add and remove data from a heap, it is not made to search for, or remove specific data.

The way a heap works is that when data is added to it the data is organized so that a minimum or maximum keyed data quantity will be placed at the top of the tree and the beginning of the array. A heap that manages keyed data so that the minimum key value is at the top of the tree is called a min heap and a heap that manages keyed data so that the maximum key value is at the top of the tree is called a max heap. So in a correctly structured min heap, the first keyed value will have the lowest key value in the data structure, and for a max heap, the first keyed value will have the highest key value in the data structure.

However, once you are past the first item, things get a little messier. A heap is not a Binary Search Tree in that the left child is not necessarily less than the parent and the right child is not necessarily greater than the parent. The only rule for heaps is that in a min heap for example, the two children will always be greater than the parent no matter how the children are related. It is possible, and many times probable, that the left child could be greater than the right child, but again, both children must be greater than the parent (in a min heap).

Side Step: Tree Characteristics

Now with a brief description of heaps behind us, we need to consider tree characteristics so we can manage another requirement of heaps. As you have seen previously, trees can come in many shapes and sizes. However, there are a couple of tree types with which you must be familiar.

First, there is a full tree. An example is shown below.

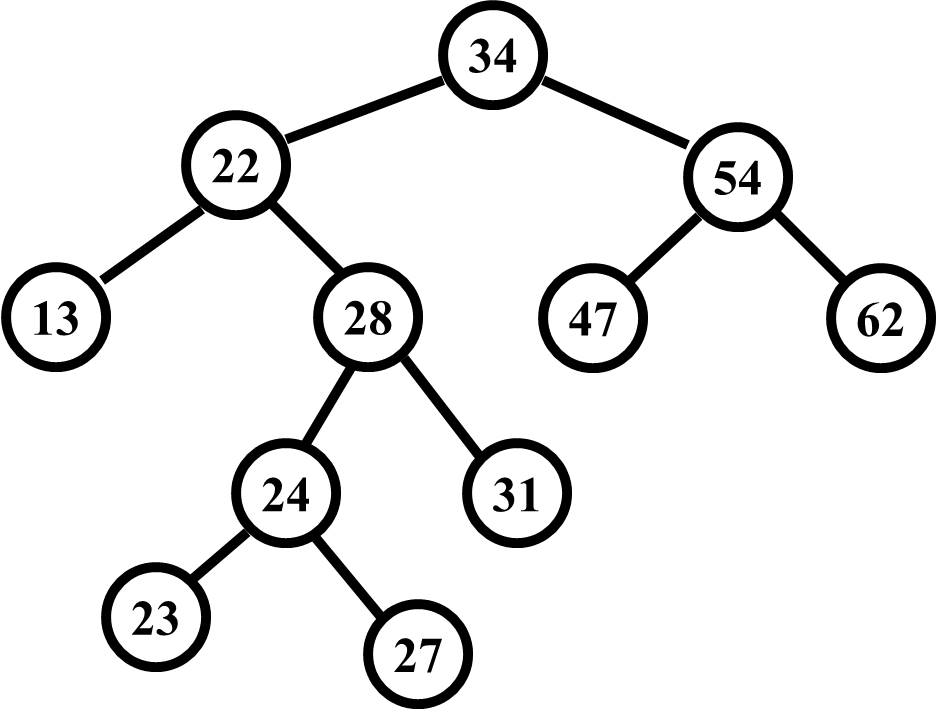
The above tree is a full tree because every node either has two children or no children. A full tree cannot have any nodes with only one child. To be clear, the nodes can be all over the place and the tree may be significantly unbalanced but every node either has two children or no children. That's a full tree.

Now consider a complete tree, shown below.

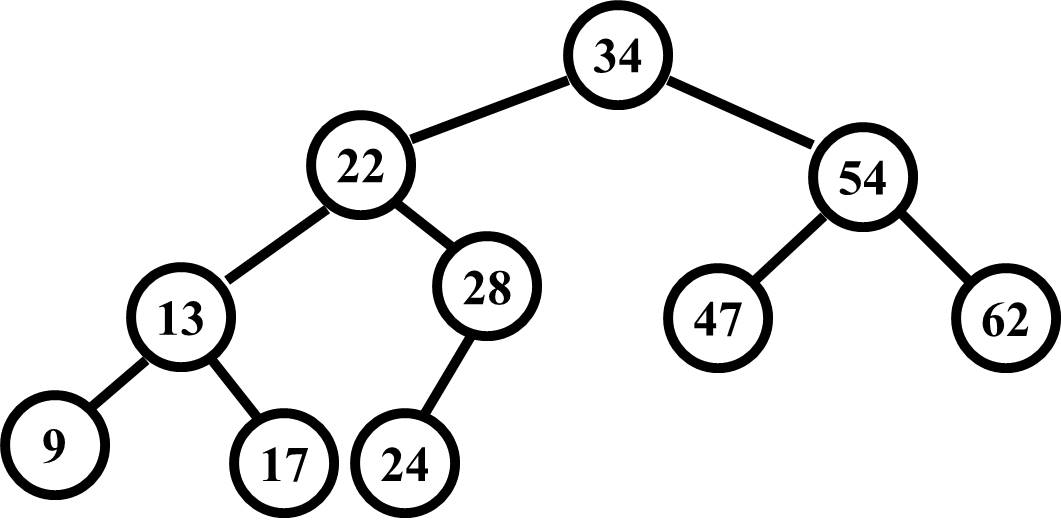
The rule for a complete tree is that all the levels are filled down to the bottom row of nodes. That row must fill in from left to right. Unlike a full tree, a complete tree allows for zero, one, or two children, but again, the nodes are added from left to right. Note that it is possible that the bottom row of nodes may be filled in completely from the left side to the right side. This is a complete tree as well. Just know that the next node from a filled bottom row condition would be added at the far left to continue with the left to right requirement.

Completing The Heap Requirements

Now that you are familiar with full and complete trees, you need to know that the tree structure of a heap must be complete. This will support the management of the nodes in an array.

So, what does a tree in an array look like? Consider the following.

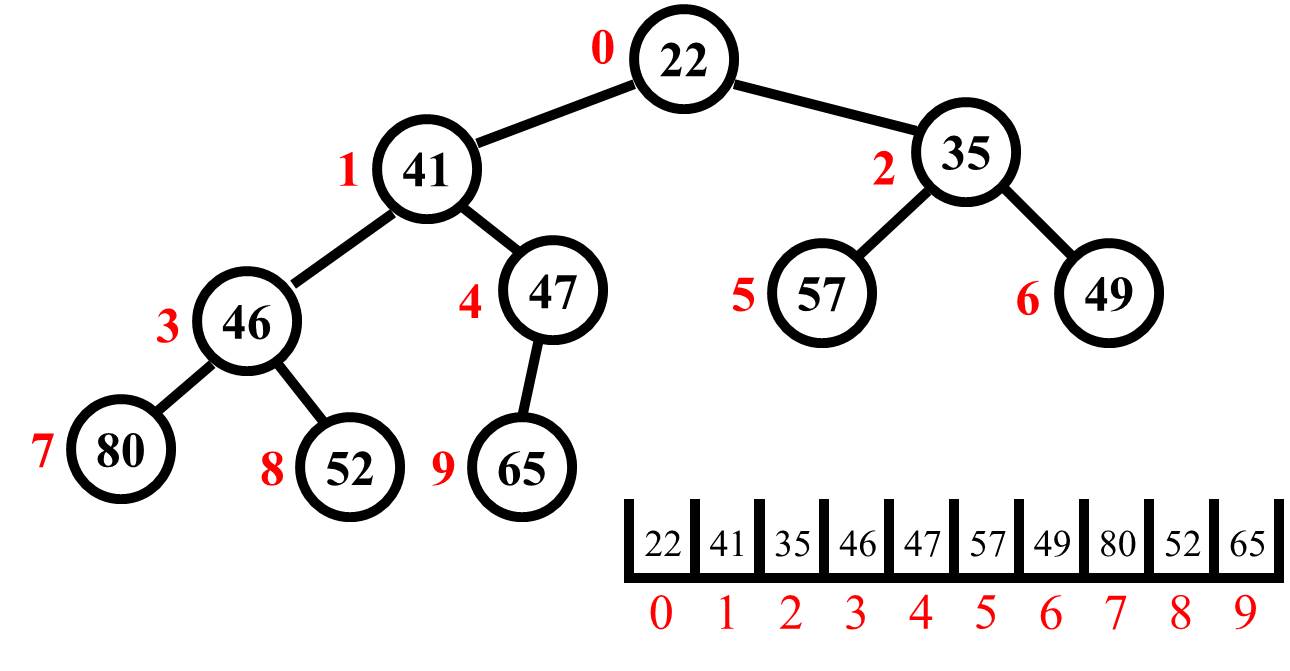
The array is real, and it is the data structure that will actually hold the data. However, the data will be organized structurally as a tree for purposes of the heap strategy. But how do you treat it as a tree, you ask? The answer is pretty cool.

If you look carefully, there is a mathematical relationship that uses integer arithmetic between each of the children and their respective parents. For example, if you take the value 47 at index 4, subtract one from the 4 and divide by two, you will get the index of the parent (1). The same goes for the 46 at index 3, subtract one from the 3, divide by two, and you again get 1. Try this with another two or three child nodes and you will find that the array element does not need to hold parent index information; it can be calculated.

And as you might expect, the indices of the children can also be calculated. If you look at the value 35 at index 2, and you multiply the index by two and add one, you will get the index of the left child. If you multiply the index by two and add two, you get the index of the right child. Again, you should try this with other nodes to make sure it works for you.

Making An Array Into A Tree

Now why would you do this, you ask? Because now that you imagine the structure as a tree, you can iterate from child node to parent node or parent node to child node, jumping over several elements in the array that you do not have to consider. Think about the element at index 549. It's parent index is 274. This means if you need to move from parent to child, or versa vice, you will be skipping 275 elements to get there. This also means that instead of linear iteration over the data structure, you will now have Log₂N operations when you conduct addition or removal of data. Again, back to the difference between 1,000,000 possible iterations in a large data set to 10 for the same set.

To repeat from previously in this topic, this is a very powerful approach to applying a tree-like data structure to an array but at the same time, thanks to the simple rule that the children are greater than the parent (in a min heap) without any left/right considerations, the heap can really only do one thing: Give you the smallest key value in the list (in a min heap) on demand. This strategy is very well suited for a thing called a priority queue which does exactly what it says. If one person is more injured than another in a hospital ER, it doesn't matter when the person comes in, she or he will be treated sooner (or with what's said to be a higher priority) than others with less serious conditions.

Small side note: You will likely hear or read about a thing called a "heap sort" which really isn't a thing. While it is true that every value coming out of a heap will come out in order, and in fact if you empty a heap all at once, the data will be ordered, this would be much like starting and stopping your car engine every time a tire completes a rotation. There are much better ways to sort . . . and at this point, you already know what most of them are.

The next two topics will cover adding data to a heap and removing data from a heap. Using the tree-like structure of the heap, you will find that the process for managing this is pretty easy, very effective, and fast. Check it out.