A Different Kind Of Tree

How It Works

Instead of being a binary tree, the Two Three tree has nodes that can hold two data values and that have three reference links to nodes below*. The interesting thing about the Two Three tree is that the bottom is always flat; in other words, the bottom row of leaves are all at the same level. When new nodes must be added, they are added at the top of the tree as shown here.

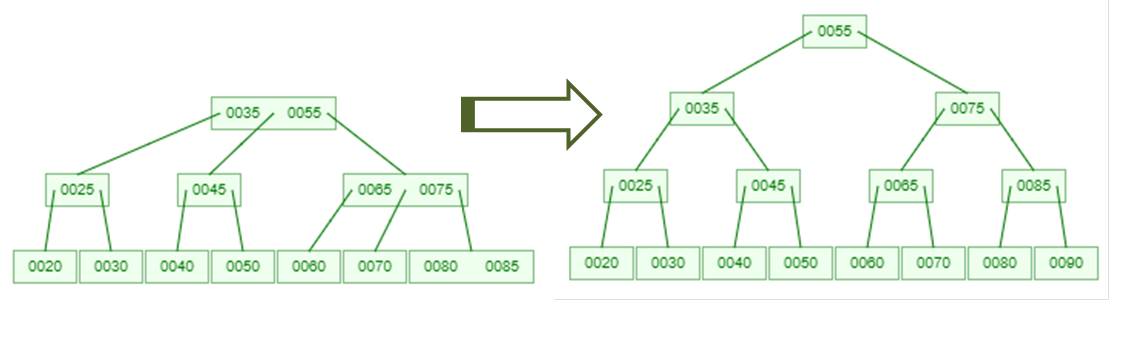
Image Credit: Screenshot from USFCA animation, David Galles, Curator

As mentioned the bottom of the tree is always flat (i.e., the lowest leaves will all be at the same height in the tree) and the tree is always fully balanced thanks to the strategy of adding a new node above the current nodes when the rest of the tree cannot appropriately hold the new data. The Two Three tree can actually be related to a Red Black tree so it is a little more complicated than the other self balancing trees but as mentioned previously, complicated just means you handle small parts of the process one at a time and from there you can get the whole thing programmed. Complicated does not mean difficult.

*With the introductory discussion provided, there needs to be a small correction here. The nodes are actually capable of holding one more data item and one more reference link than specified. For example, the Two Three nodes can actually hold three data items and link to four nodes below. However, this is only allowed during a transition, not when the tree is in its normal static state.

When a node is given a third data item, it stores it temporarily but then when the resolution process starts, one of the three values will be passed up to the parent's node to be processed there. This means the Two Three nodes must also have a parent reference and it means that the resolution process is recursive since the parent's node may now have too many values and must pass one of its values to its parent, and so on.

It should also be noted that there are extensions on this theme. There can be Two Three Four trees which can be related to Red Black Trees, Two Three Four Five trees, Two Three Four Five Six trees and so on. All of these combinations can be handled with one set of code but that gets a little to abstract for what we need to do here. The code you might look at here will be focused on Two Three trees.

Before moving on, there is a web page you should be familiar with that handles all kinds of data structures in a graphical way. The image provided above was taken from this web site, which is here. It is very worth your while to look at, and play with, this reference to learn more about most data structures, including this Two Three tree.

Future

This topic will be completed at a future point.