Simple, but Effective

How It Works

The Adelson-Velsky and Landis, or AVL, tree was the first proposed format for balancing a tree. It is not a very complicated process and it does not need some of the extra support such as a parent reference that the Red-Black tree or Two Three tree require. In a nutshell, the AVL tree incorporates the balancing process into the insertion action so that after every level of recursion going downward, the height of the tree is checked. If, from that point, the tree (i.e., the left and right children of that node) have a difference in height of more than one, actions are taken to rebalance the tree. This means that as the location for the new node is searched and recursively called to the left or right, the insertion process will go to the appropriate bottom of the tree and add the node.

After the node is added at that level, the tree checks below it for rebalance and responds as needed. Then when the method at that recursive level has resolved its balance, the method ends and the method that called it is now back in play. It then checks for balance at its level, and so on. The other two strategies are recursive in that they resolve their current condition and then call the same method at the appropriate parent. The AVL strategy simply rebalances as each level of the recursion -- that was already used for searching and inserting -- completes.

Another unique character of the AVL tree, as mentioned previously, is that it does not allow a height difference of more than one at any level. The Red-Black tree will allow a difference of two and the Two Three has a flat bottom; that is, there are no differences in height from any give node to the bottom of a Two Three tree.

Before moving on, there is a web page you should be familiar with that handles all kinds of data structures in a graphical way. The image provided above was taken from this web site, which is here. It is very worth your while to look at, and play with, this reference to learn more about most data structures, including this AVL tree.

The Inserting Process

The first part of the process is a standard insertion process as you might see in many Binary Search Trees. Consider the following code.

   // check for current node null

      // return a new created node

   // otherwise, check to see if the new value is less than the current node data

      // make the recursive call to the left child
      // and assign it to the current node's left child

   // otherwise, check to see if the new value is greater than the current node data

      // make the recursive call to the right child
      // and assign it to the current node's right child<

   // otherwise assume the value is already in the tree

      // update the current node with the new data

Note that one, and only one, of these four actions will be taken. When this part of the code has complete, the new value has been inserted, or if it was the same key, the data at the found node will be updated with the new data.

Finding The Balance Factor

This part is usually a line or two of code but it is where the decision-making action occurs so it is worth considering. To decide if balancing needs to occur at this point, the heights of the two child trees must be found and the mathematical difference between them will be used. The balance factor is found by subtracting the left child's height from the right child's height.

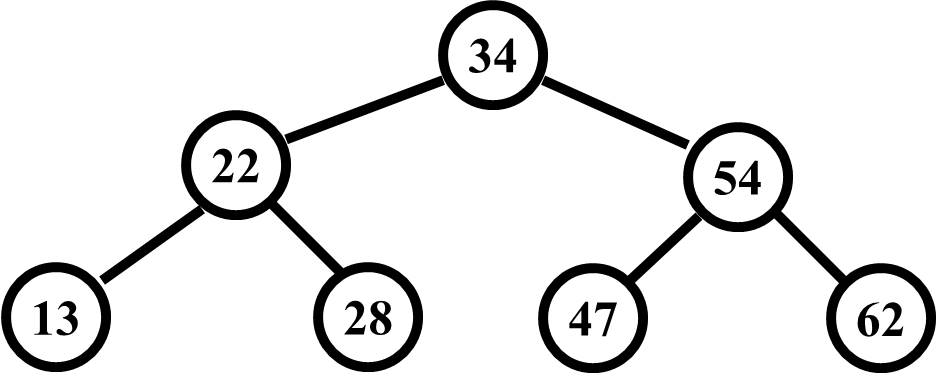
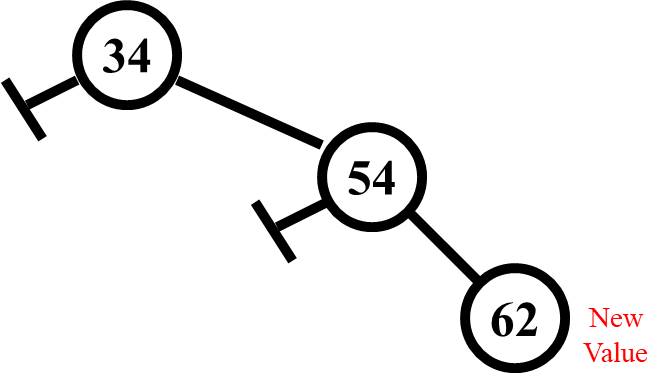
If a tree has two equal height children as shown here, the balance factor is zero (i.e., left child height - right child height is zero). The height below the value 34 is 2 on both sides, so 2 - 2 is zero.

If the left child of a tree has a larger height than the right side, the difference is again found by subtracting the right side from the left side. Consider the following tree.

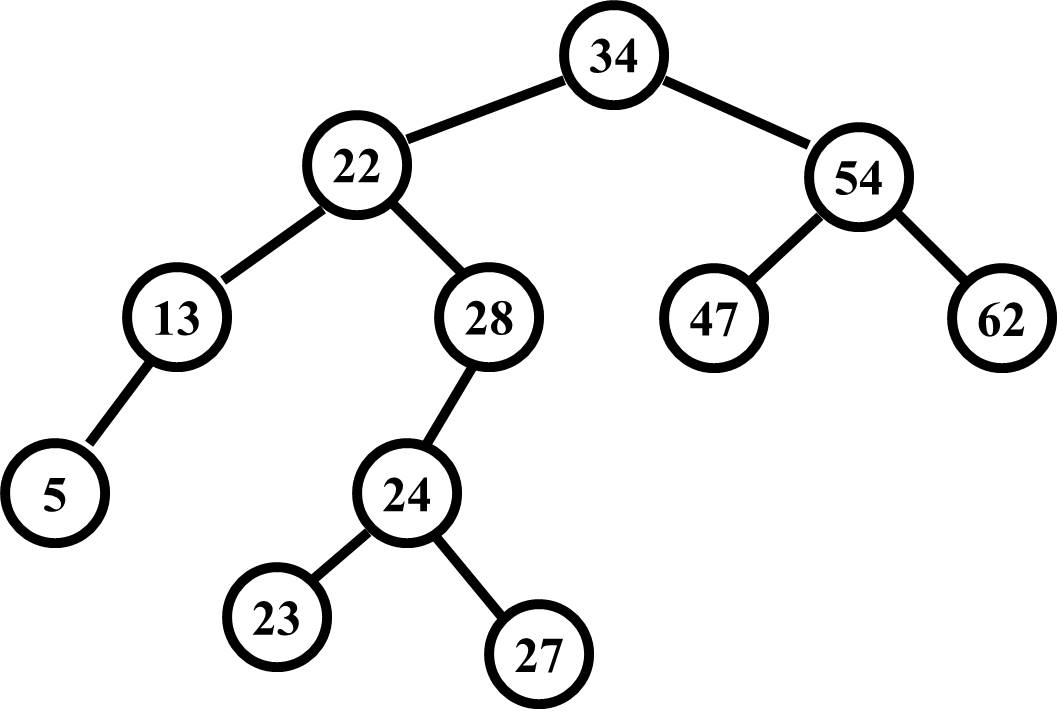
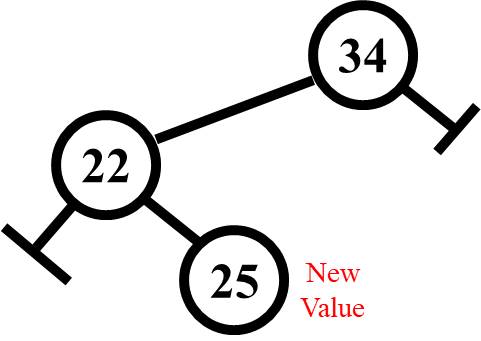
Again viewing from the 34 node, this tree has a balance factor of positive two (2) as a result of subtracting the right height (two) from the left height (four). The difference of two is important as will be noted soon.

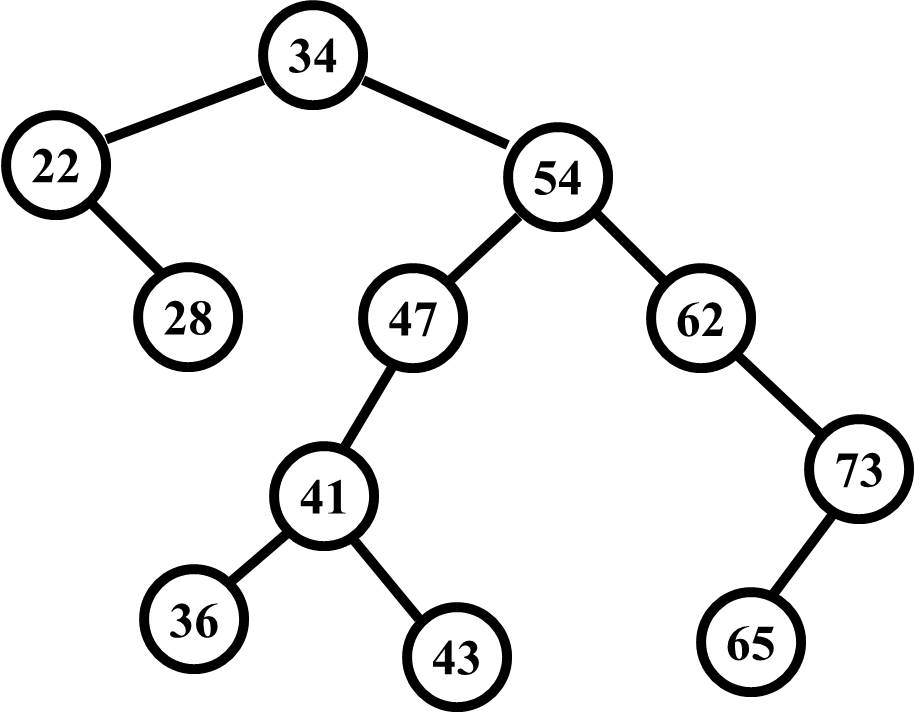
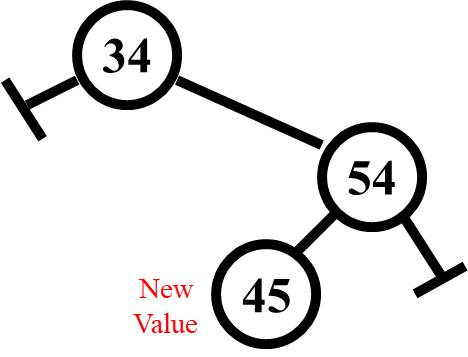
From the 34 node, this tree has a balance factor of negative two (-2) since the right height (4) subtracted from the left height (2) will resolve to -2.

The code for this part is pretty simple.

   // find the balance factor and assign it to a variable

Decide Whether To Adjust

Once the balance factor is found, there are five possible conditions:

• If the balance factor is not more than one or less than negative one, nothing happens and the method completes


• If the balance factor is greater than one, and the new data is less than its parent data, there is a Left Left condition



• If the balance factor is less than negative one, and the new data is greater than its parent data, there is a Right Right condition



• If the balance factor is greater than one, and the new data is greater than its parent data, there is a Left Right condition



• If the balance factor is less than negative one, and the new data is less than its parent data, there is a Right Left condition

Remember that after this the method completes, the method that called this one will do the very same thing at its level. This balances the tree up as high as is needed.

Now We Rotate

Once the imbalance has been identified, the nodes are "rotated" or repositioned in a way that balances the tree, at that particular node level. The rotation process itself is just a few reference assignments that relocate the nodes. Here is an example of a right rotation that resolves the Left Left condition.

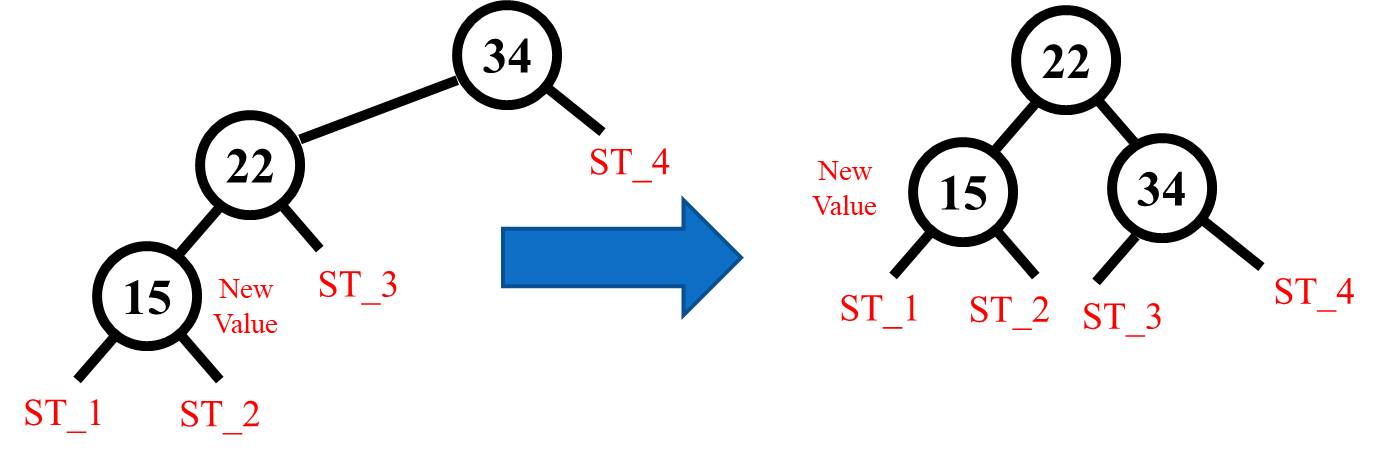
Note here that while the children of each of these nodes may be null, they may also have other subtrees below them. All of these subtree links must be considered. The code for rotate right is provided here.

   // assign the left child (22)'s right child (ST_3) to a temporary

   // assign the reference of the (34) node
   // to the left node (22)'s right child

   // assign the temporary to (34)'s left child

For the Left Right condition, the data has to be rotated left first which will result in a Left Left condition but then you can use the rotate right operation to resolve that. Here is an image of the left rotation for a Left Right condition.

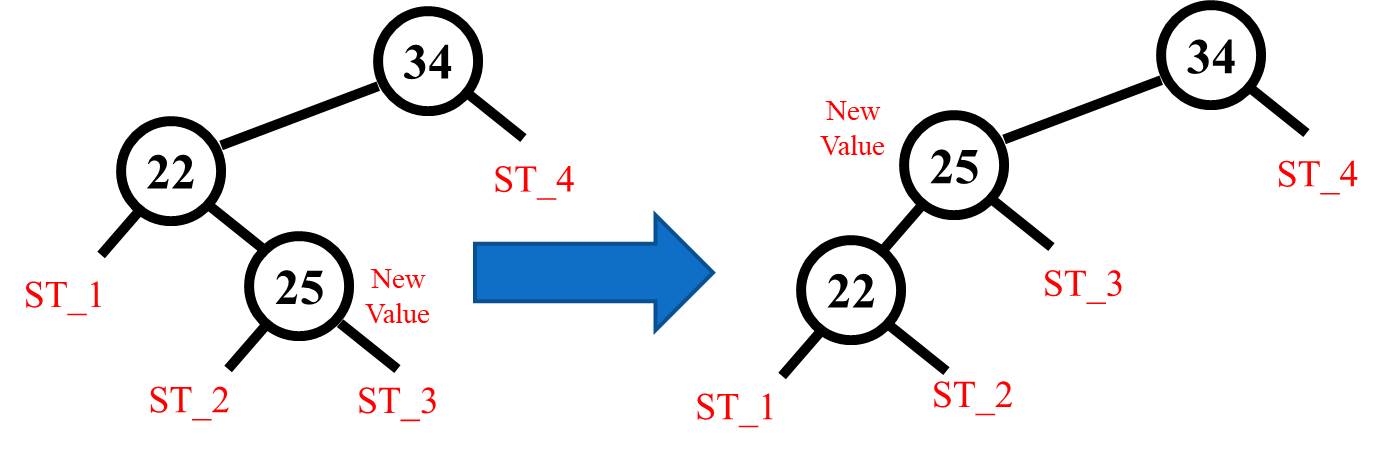
And the code for this one is as follows.

   // assign (25)'s left child (ST_2)to a temporary

   // assign the reference of the (22) node
   // to (25)'s left child

   // assign the temporary to (25)'s right child

Now since this code is provided as a general reference, the thinking part of this is to figure out what parameters need to be passed into the rotate left and rotate right methods to accomplish these tasks. However, if you think through these parameters, you can easily write rotation operations that will use relatively simple coding like that which has been provided for all four conditions. There is no need to create different code for the differing rotations. You should be able to write one left rotation action for both left rotation operations and one right rotation action for both right rotation operations.

That's About It

To review, the insert process conducts a standard BST insertion, but before it completes, it checks for unbalanced conditions below itself. If it finds a difference of more than height one, it identifies the conditions and rotates the nodes as needed to rebalance the tree. This is conducted by every method that is recursively called down to the point of adding the node so as each recursive method ends, the one that called it takes over and conducts the balancing process at its level. The tree will be balanced or rebalanced all the way up to the original method call that occurred at the root level.

Again, as one of three kinds of self-balancing trees, the AVL tree has its own characteristics that set it apart from the other two, and like the other two there are a couple of complicating conditions. However, each of these is easy to tear down and address individually. And also remember that there is too much here to try to memorize. The smart money is on the folks who take the time to understand what is happening, and from there, converting it to code is really not difficult.

One final note. There is very little on the Internet that is helpful to serious programmers. However, one recommended reference is the Geeks for Geeks website. This site has a few flaws as well but for the most part they are true to the Computing Science they present. You can find the web site for AVL trees here, and remember that you can see AVL trees in action at the USF website here.