Upping The Data Access Game

The Concept of Binary Search Trees

The linked list was your introduction into generally linked things. You no longer have variable names or element indices. You have a head reference and the rest of the list which you can iterate across be referring from one given node to another linked node using one or more working references. In this sense, a Binary Search Tree (BST) is the same thing. You can only get from one linked item to the next by using the reference data being held by the node that is currently being referenced. However, a BST doesn't link to just one node, it links to two, which have to follow a simple rule. The left node of a parent in any given node combination must have a value less than the parent, and the right node of a parent in any given node combination must have a value greater than the parent. Consider the following.

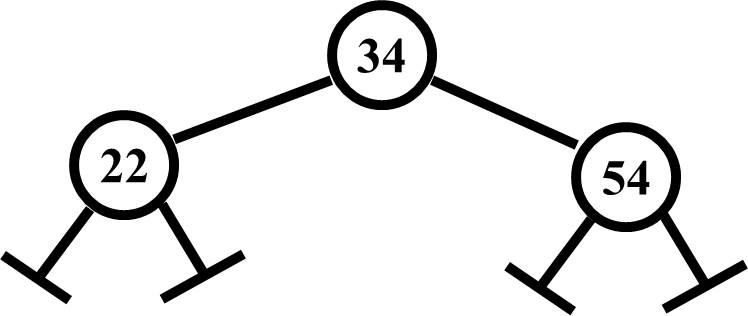
One thing to mention here is that this is a node set in a Binary Search Tree (BST). It is possible to have just a simply binary tree which would have a parent and two children but no particular rules about how the children relate to the parent. It is also possible to have a binary tree with other rules that don't make it a BST but do make it a tree with other uses. You will see an example of that later in your Data Structures studies.

You will note that the two links at the bottom of the node combination are the same as the null links in a linked list and they mean exactly the same thing, that there is no further data from that node, in that direction and beyond. In addition, if a given node in a tree has no children (i.e, both child links are null), it is considered a leaf node. This will be handy to know as you expand your knowledge of trees.

So, Why?

You should know that if you can have a binary tree, you can also have trinary tree, or a quinary tree, or even a hexary tree. You are only limited by how many child references you have in your data structure, and in fact, there is no limit on that.

So why create a binary tree? The answer is in the two. If you have a binary tree and a decision point at every node, each time you make a decision, you divide the data quantity by two. For example, if the tree shown previously on this page had 1,000,000 values linked to the left child and 1,000,000 values linked to the right child and you ask the simple question, "Is the value I am looking for less than the value at my current node, which is 34?" If the value you are looking for is less than 34, then you will search down the left side of the tree and ignore the 1,000,000 values on the right side of the tree. This brings us back to the Log₂N relationship that was discussed previously in this reference. Dividing by two, which is called a "Divide and Conquer" strategy, means one could find a value in a list of 2,000,000 values in 11 searches or less rather than potentially 2,000,000 searches if a linear search was conducted with an array or linked list. Pretty Cool.

So if two is good, isn't three, or five, or even sixteen even better? Actually in some cases, these choices might be better. However, the simplicity of a "less than"/"greater than" test means the code is not complicated and does not cost a lot of overhead in the searching. In most cases, simple wins over other strategies, although you will see an alternative or two in the next chapter.

Naturally Recursive

The next obvious question to ask is, how does one get around in a BST? The answer has really already been provided in the previous discussion. A search is conducted for data, and a decision is made at each node that is accessed. However, the magic of a BST is that every node combination within a larger tree is its own tree. Other than leaves, every combination has a parent and one or two children, and leaves themselves are still children. So the solution to work with one node is the same solution needed to work with all the nodes, which of course makes recursion an easy choice for traversing a BST.

What's In It?

An example of the code for a BST node is provided here. Obviously, there can be some small differences but this is pretty much what will be in the class.

   public BST_NodeClass()
      {
       SomeDataType data;  // whatever data is being stored

       BST_NodeClass leftChildRef;

       BST_NodeClass rightChildRef;
      }

This is it. And as mentioned, while there may be small variations in how the data is managed, this is pretty much all that is needed in a BST node. Essentially the data and two child references instead of the one next reference from a linked list. Again, not complicated.

Don't Put Away Your Pencil

Binary Search Trees are very slightly more complicated than linked lists, by the addition ofone reference variable. That is to say, BSTs are not that complicated. However, like linked lists, there is very little chance you can solve problems and/or manipulate BSTs without drawing pictures. Many methods that manage BSTs are simple and don't have that many lines of code, partly because there isn't that much to manipulate at any given point in a tree, and because you can use recursion in almost all the operations you will conduct with trees. No matter what action you wish to conduct with BSTs, you must always start with a picture AND you must always verify that your picture represents all the parts of that action, to make sure your code writing doesn't take too long, and to make sure it is going to work. Let's move on to some of the BST operations you can implement.