Brute Force Operations, Example

Getting Queens to Play Nice

The eight queens problem is an interesting study with little value other than to fool around with computing. However, the fooling around part is what makes thoughtful programmers good at what they are doing. And for that reason, it is very worthwhile to consider this.

The big picture goal is to place eight queens on the same chessboard in such a way that they don't conflict with each other. Those folks familiar with the game of Chess know that a queen can not be in the same row or column as another queen, and no queen can be on the same diagonal as any other. As you might expect, more queens added to the board makes finding a non-conflicting location more difficult. And as you might also expect, there are a lot of possible combinations of where the queens can be with respect to each other. This is the combinatorial part of the business mentioned in the previous section.

Here is the board starting out with one queen.

You have been given the big picture goal but now you need to follow the small picture goal. The method that will accomplish this whole process has one goal to accomplish: Place a queen. The method will be given a column, it will start at the top of the column every time it is called, and it will iterate from the top to the bottom of the grid looking for a location that does not conflict with the other queens. Once a conflict-free location has been found, the method has accomplished its goal, and will now call itself (i.e, the same method) with the next column over. This method will again start at the top, iterate down to find a location, and when the location is found, it will call itself again.

But . . . What happens if the method tries all the row locations in the given column and none of them work? That's easy, the method just gives up and goes away. However, the game is not over because that method had been called by itself previously so the previous method call picks up where it left off and continues looking for a new location since the last one does not support a working solution. This is the backtracking part. Nothing is called, and no action is taken. In fact, it is the opposite. When a method has failed, it just stops and lets the previous method pick up where it left off prior to calling the method that failed.

Here is the board partly loaded with queens.

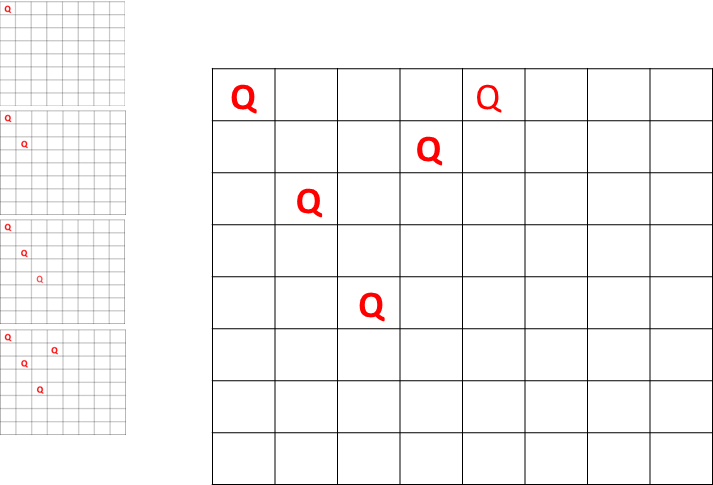
You can see that each queen is not vertically, horizontally, or diagonally in conflict. You can also see that the methods that have been called are stored on the Operating System (OS) stack. When the first queen was placed and that method called the method with the second column, the first method -- along with its state, or current conditions -- was stored on the stack. Then when the second queen's spot was found, the second method was stored on the stack with its state data while the third method went to work. And so on. The current condition for this image is that the states of four methods have been stored and the fifth-called method is getting started with trying to place a queen.

What will happen as the program progresses is that each method that succeeds will call the next one and the calling method will be placed on the stack. But . . . to continue with the answer to what happens if any given method fails to find a conflict-free spot for the queen? Again, the working method fails, and the most recent method will be pulled off the OS stack and go back to work from where it last left off, looking for a safe place for its queen.

The progress of the program is that when a method is called, it seeks a location; if it fails, it quits and the previous method takes over; and the program conducts a forward and backward process until a solution is found, if there is one. Note that once a complete solution has been found (i.e., all the methods have finally succeeded to the last queen), all the methods will come off the stack after each method has completed. Here is an example solution for this problem.

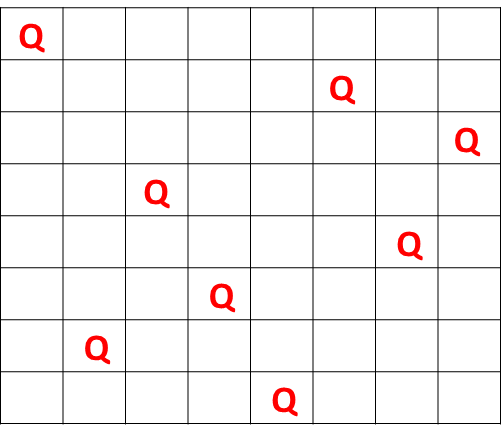
As you will note, none of the queens is aligned vertically, horizontally, or diagonally with any of the others. There are twelve fundamental solutions to this problem but many more if you rotate the board 90, 180, or 270 degrees and consider those solutions.

Check out this video to see an animation of this problem. It is worth your time to take notes and follow the step by step process. It's definitely not difficult, but it is complicated (and combinatorial). There are two more examples provided in the next sections but be aware that this is a process that can be used on many combinatorial problems.