Connecting The Dots

From Here To There, But Differently

You know that graphs provide a different way to represent data. On the other hand, you have been here before. Remember Binary Search Trees (BSTs)? They are a form of graph. And if you recall, you could systematically work your way through a BST in at least three different ways; this was a process we called traversing the tree.

Well, if you can do it with BSTs which actually are a form of graph, you can do it with generalized graphs, although the traversing will look a little different. In a BST, each node had two children so you could treat every node (vertex) the same as you passed through it. Now in generalized graphs, a vertex might have one or more edges from any given vertex in a connected graph, and you may not know how to consistently and systematically get to every node. Fear not! Computer Scientists have worked that problem out for you.

But how you traverse a generalized graph depends on what you want to get out of the traversal. Consider a vacationer looking to visit some pleasant upstate New York farms. If that vacationer happens to be in Arizona and she only has the one or two weeks of vacation permitted, she will want to get to New York as fast as possible to get started with touristing. For this part of the trip, she will want to use a Depth First Search or DFS strategy which means she will go as far, and as fast, as she can go to get there. Her mode of transportation is commercial airlines so she will want a flight that gets to New York as soon as possible passing through the fewest vertices possible.

However, once she gets there, she will want to spend some quality time in the area, and because this is a one time kind of trip, she will want to be sure to visit each and every little farm in the local area. This means she has to apply a systematic approach to visiting near neighbor farms, and she will implement the Breadth First Search or BFS strategy to make this happen

First, a couple of notes. The terms are Breadth First and Depth First Search when the title of this topic has the word traversal in it. To be clear, there are conditions where a programmer will actually use one of these strategies to search for some given data. However, in almost every reference where the acronyms BFS or DFS are used, the users actually mean traversal. So, while we use the the acronyms that end in S, we really mean for them to end in T.

The next thing to note about these traversals is that they are systematic, consistent, and complete. Both traversal operations MUST visit every single vertex in the graph; none can be missed or overlooked. This is the critical part of these strategies whether they really are used for searching, or they are used for traversing. Let's check them out.

The Breadth First Traversal (BFS)

You can kind of think of BFS as spiraling around and away from the original vertex in small concentric circles, even though they usually aren't circles. As you become more familiar with this strategy you can think of the path in your own way but the concentric circles visual will help until you get there. Let's look at the graph used in the previous topic again.

The first thing to note is that, as you noted in the previous topic, every vertex has its own list of adjacent vertices or near neighbors called its adjacency list. This will be used extensively during this traversal. However, to keep things consistent, we will also assume that when we acquire a new vertex from an adjacency list, it will be released in alphabetical order. For example, when the A vertex below requests a vertex, it will get each one in alphabetical order, which would be E, M, R, and T. This is not a standard rule in these searches/traversals but it is a policy we will use so that our results are consistent every time.

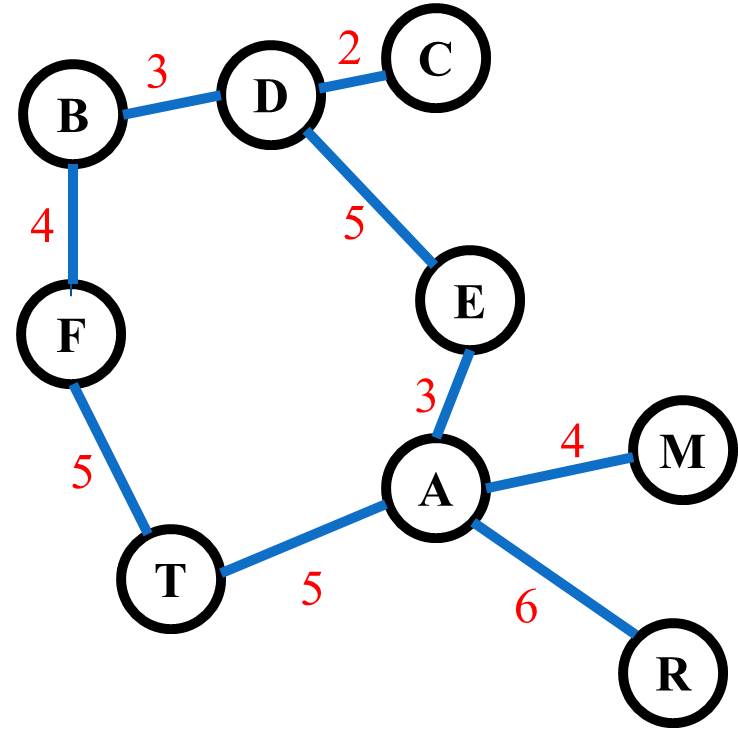
Let's also assume we will start at the letter F. With either of the traversals, it doesn't matter where you start so you can pick any one of them. This strategy uses a queue. Having started with the F, the operation will enqueue vertices as they are visited, and then dequeue them in order. In this case, the F will enqueue its neighbors B and the T and when it has completed enqueuing both (all) of its near neighbors, it will drop out. Then, since the B was enqueued first, it will enqueue all its new adjacent neighbors (i.e., it won't reenqueue F); this will be D. Then when B is done the next vertex available is T. T will enqueue A and then drop out, and the process will continue in the same manner until all the vertices have been visited.

The visitation order will end up being: F, B, T, D, A, C, E, M, R. The traversal process keeps each vertex transition from going very far at any given step.

The Depth First Traversal (DFS)

The DFS is almost the opposite strategy in that the vertex transitions try to go as far as they can go as fast as they can get there. This strategy uses a stack. Let's look at the graph again so it is easy to follow.

In this case, the F would be placed on the stack and then its value would be checked (i.e., peekFront instead of pop) to find its nearest neighbor. This would be B (alphabetically before T) so B would be placed on the stack. Then B would be checked (not popped) and his first near neighbor is D, that now gets pushed on the stack. D gets viewed and gets C as a near neighbor but C doesn't have anywhere to go, so C is popped. Next D gets its next near neighbor which is E. E is viewed and his next neighbor is A which is pushed on the stack. A is viewed and finds M as a near neighbor but M has no other neighbors so M is popped. The A is viewed and gets R as the next neighbor but R has no other neighbors and is popped. Once more A gets T which is pushed on the stack but when T asks for a neighbor, F has already been used so T is popped, then A is done and popped and E is done and popped and so on.

The visitation order for this DFS will be: F, B, D, C, E, A, M, R, T

While this graph is a decent size with nine vertices, the difference between BFS and DFS is much more exaggerated when there are more vertices. You should take opportunities to conduct these traversals on larger graphs to make sure you have the hang of it.

Looking Over Traversals

The BFS and DFS traversals are systematic ways to visit every vertex in a given graph. The BFS traversal tries to stay as close to the original vertex as possible for as long as possible and the DFS tries to get as far from the original vertex as fast as possible. The strategies are not terribly complicated but you will need to practice them to familiar enough to demonstrate one in a given situation, say an interview.

There are a few things remaining to look at. The first is that you can look at a pseudo code version of both the BFS and DFS here. If you follow this process systematically and carefully, you will be successful with the traversals and you can develop code for this if you wish.

You can also practice with a couple of larger graphs here and here to up your game. And finally, you can view the BFS video and the DFS video to follow the whole process step by step.

As you review the materials and the videos, and see the use of the queue and the stack, this last little tip will help you remember which goes to which. When you are working directly with the traversals, you won't have any question but if you need to remember off the top of your head at some point in the future, just remember that B(readth) comes before D(epth) and Q(ueue) comes before S(tack) [B < D, Q < S] and you will always know which is used for which without having to work it all back out again.

Once again, there is so much more to studying graphs but this chapter should help get you get started with the learning, and find success with the fundamentals. Enjoy.