Removing The Data

Introduction

Removing nodes from a binary tree is more complicated than inserting nodes. However, it doesn't have to be too much more complicated. When it comes down to actually implementing the process, you just need a checklist to make sure you have covered all the possibilities. In this section, you will be provided three "Shopping Lists" that will make sure you have responded to all the scenarios that could occur in the course of the removal process.

First, The Search

The search is necessary for removal but before the removal process is considered, let's take a look at the search as its own operation. In a nutshell, you will ask if the search value is less than the current node and if it is, you will recurse to the left making sure to return the recursion. If the value is greater than the current node, you will recurse to the right and again return the recursion. If it is not less than, or greater than, the search value, then it is the search value and you can return that.

A key point for returning found data is that you must return it from the data in the tree. Very commonly you will be given an object, or part of an object, as a key to find the data. However, the key data you are using will be (obviously) incomplete. Once you have found the item, you MUST return the data from the tree so that the user/programmer actually gets back all the related data instead of just the key.

With that said, it is also a possibility that the key/data is not in the tree. If this is the case, the strategy above will run into a NULL reference sooner or later. This is not a big problem but it means that you must test the node you are currently at for NULL before you do the other testing provided above. Make sure you take care of that circumstance.

Check out the code below to see how this would work.

   // check for root not NULL
      {
       // check for search value less than local data value
          {
           // return the recursive call to the left
          }

       // otherwise check for search value greater than local data value
          {
           // return recursive call to the right
          }

       // otherwise, return the found item
      }

   return item not found (NULL)

Then, The Removal

As mentioned previously, there are several considerations to manage when you are removing a node from a tree. Let's start with the three shopping lists first, and then expand on them afterwards.

Shopping List #1 (searching):

1. Check for the current node reference to be NULL, if that is necessary
2. Check for the search value to be less than the current node, and recurse left if so
3. Check for the search value to be greater than the current node, and recurse right if so

End of Shopping List #1, the node has been found

Shopping List #2 (eliminating easy child conditions):

1. Check for the current node's left child to be NULL, and return the right child's reference if so
2. Check for the current node's right child to be NULL, and return the left child's reference if so

End of Shopping List #2, the easy removals have been resolved

Shopping List #3 (removing a node with two children):

1. Check that the left child has a right child


• if so, call removeFromMax, and transfer the data from the removed node to the current node
2. If the left child does not have a right child


• copy the left child's data into the current node and link around the left child to remove the node

(Alternate) Shopping List #3 (removing a node with two children):

1. Check that the right child has a left child


• if so, call removeFromMin, and transfer the data from the removed node to the current node


2. If the right child does not have a left child


• copy the right child's data into the current node and link around the right child to remove the node

The end of Shopping List #3 is the end of the removal process.

As you may have noticed, there are two possibilities for shopping list number three. Either one works so it is up to the developer to decide which one to use. But before you make that decision, you need to know what is happening with this part of the process. Consider the following tree.

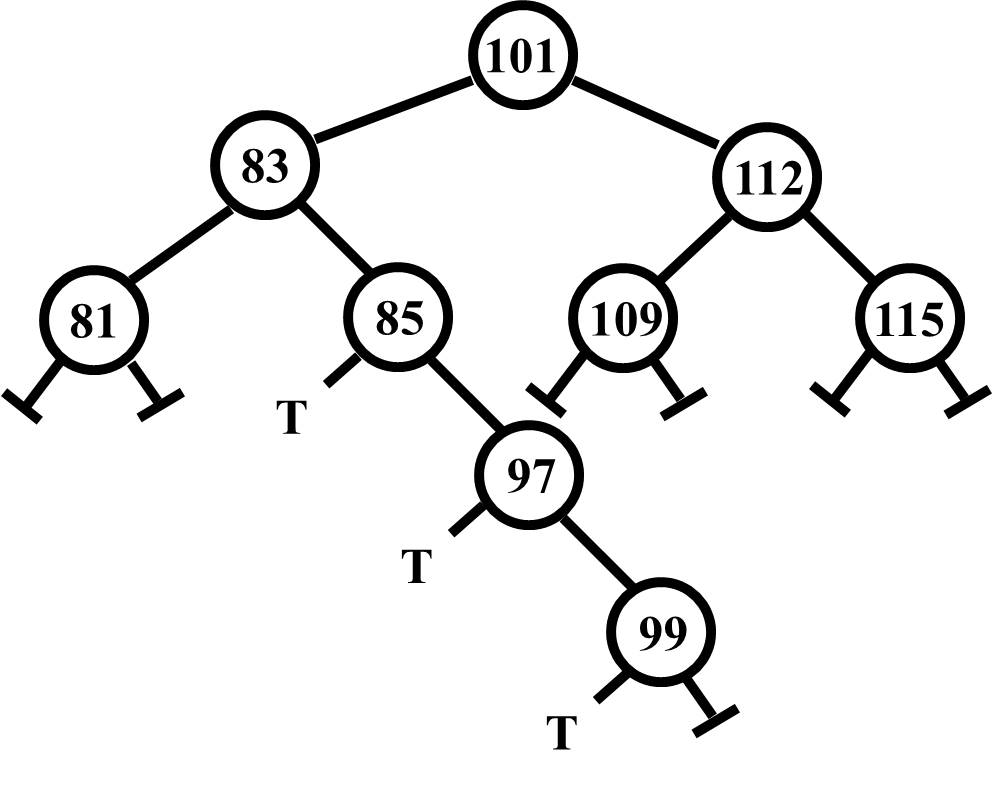
When the node to be removed has two children, you cannot just take it out of the tree or you will lose one or more connections to the children's trees. So the strategy is to find a value that is the closest it could be to the removed node and replace the data in the removed node with the data in that closest node. Now it turns out there are two "closest" nodes. The first one is the maximum or right end of the left child's tree. The value 99 is greater than any other value to the left of the 101 (i.e., the one being replaced) and the value 99 is less than any other value to the right of the 101.

The trick here then is to remove the 99 node but take its data and place it in the node where the 101 was being held. The problem is solved by calling a function named removeFromMax which removes the maximum node (i.e., 99) and returns the node with the data back up to the current location which is where the 101 is.

But you have choices. Consider another tree.

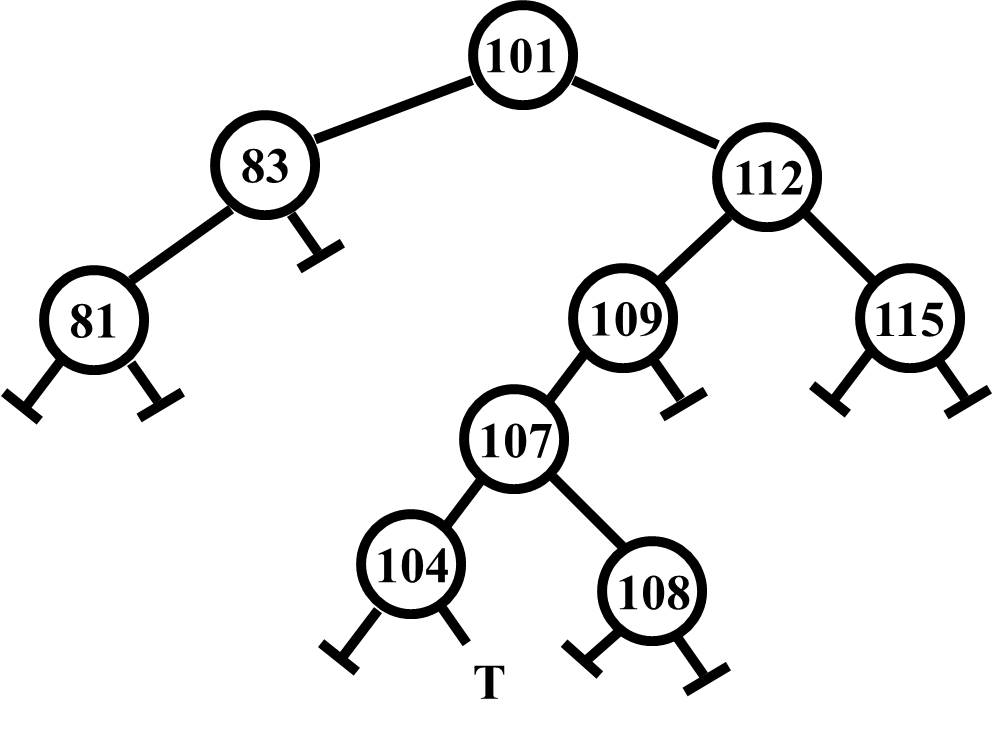
This is exactly the opposite situation. In this case, looking right from the node to be removed (i.e., 101), the right child's left tree's minimum ends in what turns out to be the closest value to 101. 104 is greater than all the nodes on the left side of the 101 and less than all the nodes on the right side of the 101 so it can be used to replace the 101. And as you might expect the function to remove this minimum node and return its data back up to replace the 101 is named removeFromMin.

But Wait, There's More

Now the two provided solutions are wonderful if the left child has right children (to find a maximum) or the right child has left children (to find a minimum). But what if they don't? What if the right child has no left children as shown here?

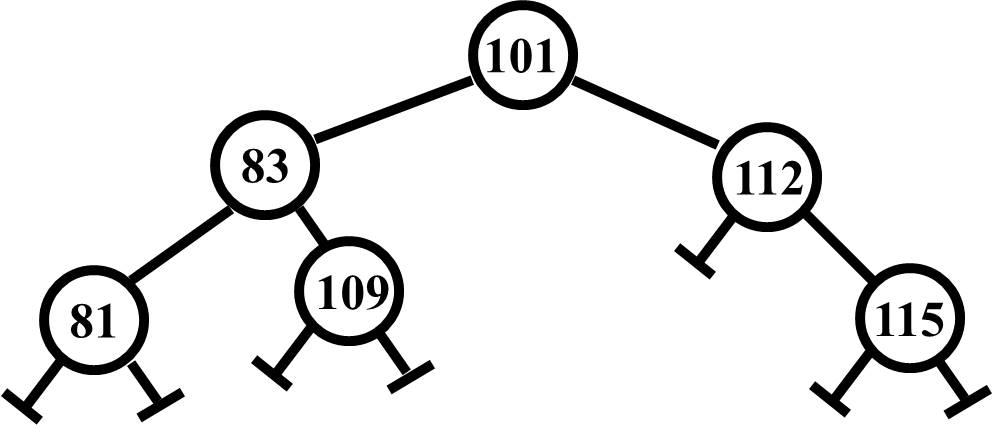
It turns out that this is even easier. You take the data from the right child and replace the 101 with it, and then you link around the right child to remove the node, as you can see here.

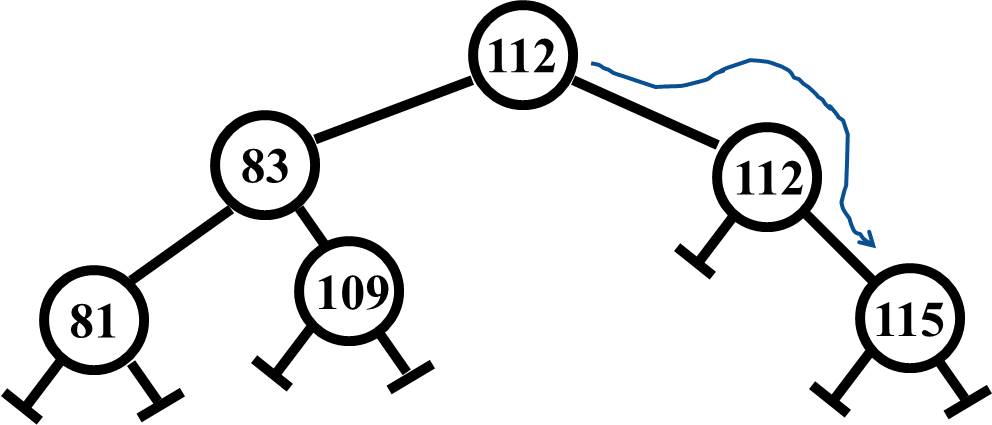
The right child that held the 112 uses its data to replace the 101, and then what is now the 112 node links to the right child's right child to take the unecessary right child out of the tree.

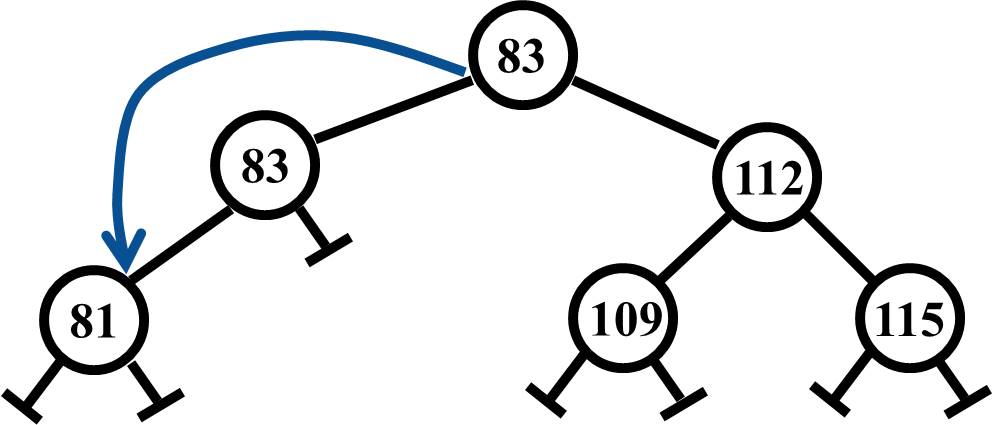
In this scenario, you take the 83 from the left child, replace the 101 node with it, and then link from the (now) 83 node to the left child's left child, and the tree is healthy again. Again for both situations (i.e., the 112 and the 83), note that they are in the correct location since all the data to the left is less than these values and all the data to the right is greater than the values

But Wait, Which One Do I Use?

The answer to this is that from a programming point, it doesn't matter. You can use whichever side of the removed node, and whichever removeFrom... you like UNLESS the requirements for given project specify that you should use one or the other. Then, as always, you follow the specifications.

Wow, That Seems Complicated

Yup, and it is. But it is not difficult. Complicated is an easy problem to solve; you just tackle each part of the larger system one at a time in this case using the three shopping lists, resolve each issue and move on. Difficult is another matter but in most cases, while Data Structures does have some complicated things, none of them are terribly difficult. Rise up and conquer.

Another Slight Sidestep: How Large Is The Tree?

When adding or removing data from a BST, one of the considerations for trees is how large it might be. And the word large is relative. If you need to know how many elements are in the tree, you can conduct a traversal of any of the three kinds and you will be able to find the number of items.

But one measurement of trees that can be helpful is the tree height. Among other things, the height of the tree is also the maximum number of recursive calls for adding or removing data from a tree. Specifically, the tree height is a measurement of the longest distance between the root node and the bottom of the tree at its lowest point. The first thing to know about height is what it really means. The best way to think of tree height is the number of legs, or what we will later call edges, between a given node and the bottom of the tree. The following tree, also seen above, has a height of two. This is because the longest distance between 101 and the lowest point only has two edges. You can track this three different ways and get the same count.

However, if you have an out of balance tree such as the following, the longest path to the bottom has four edges between the root node and the bottom, even though there are no other branches.

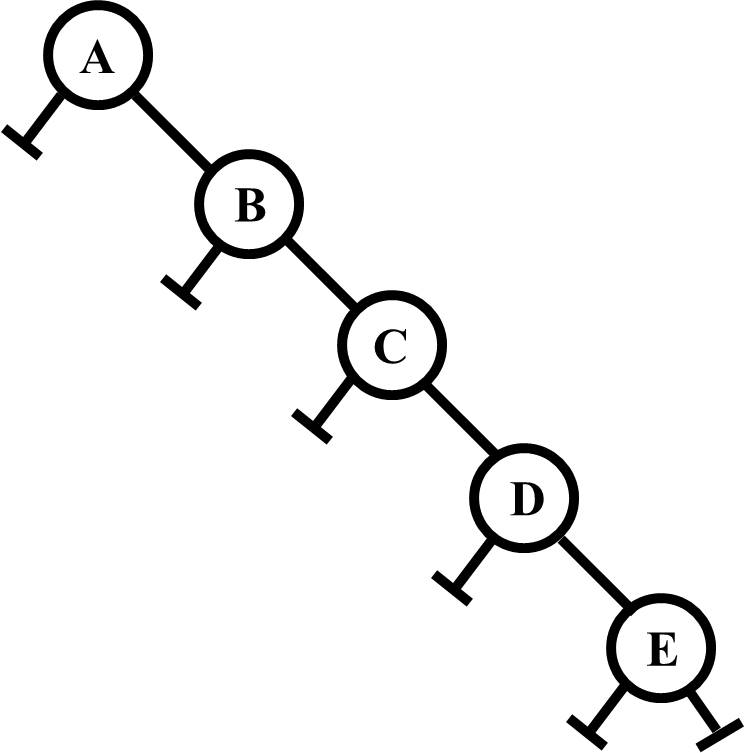
So if counting edges is the answer, what happens if there aren't any edges? There are two rules to follow here:

1. A completely empty tree (i.e., no node at all) has a height of -1,


2. A single node with no children (i.e., no edges, aka a leaf node) has a height of zero.

This will become more important as you learn more about trees.

So the next obvious question is how do you measure the height of a tree? And the answer to that one is: A) Recursively, and B) Thanks to recursion, quite easily. Consider the following code:

   // check for the current node not being NULL

      // return 1 to count the current node
      // added to the maximum height of the two trees below

   // otherwise, if the current node is NULL, return a -1

Think about it. The height of an empty tree (i.e., a NULL node) is -1, so you return that for a current node reference of NULL. Otherwise, you find the maximum height of the left and right children, add one to that to count for the current node, and return your findings. Recursion, and this algorithm, are really cool.

Wrapping Up Removal

It is not uncommon for interviewers to ask a candidate how to remove a node from a linked list or a BST during the technical interview. You should be ready for this because some folks think this process is difficult. It's not. If you keep the three shopping lists in mind, you can turn that into code (in any programming language) at a moment's notice. Trying to memorize code simply doesn't work because that is not the only question the interviewers are going to ask you. Think about how it works, turn it into code, and move on . . . as their new employee.

Since there are two options for replacing a node with two children, there are two videos for this part. The one for using the left child and the find maximum is here, and the one for using the right child and finding the minimum is here. Enjoy.