Real Computing Science

Computing Scientists like to study what makes computing algorithms work, and what makes them work better, and sometimes what makes them not work as well, as comparable algorithms. This is one of the reasons the term "Computing Science" is commonly used in this reference since these analyses do not require a computer. They just require thinking . . . that's the science.

First, Some Rules

In the computing/thinking business, some models need to be used to represent things a computer could manipulate. For example, a computer might manage a large number of people, or it might manage a very large number of tickets sold for an event. Computing Scientists don't really care what is being manipulated because they are more interested in how many "things" a program (algorithm) will be manipulating.

So, as you have read in previous sections, they came up with the concept, and the symbol, N. To Computing Scientists, N just means the "number of things that will be manipulated". If a grocery store wants to keep track of frozen peas or cans of tomatoes, they will request a program that does this. However, to Computing Scientists, peas, tomatoes, tickets, and people are just things that will be manipulated by the program: N.

The next question is how is this used and what does it matter? Great questions - take a look at the next topic.

Counting Steps

Consider the following code.

   int findNumberOfCans( int numberOfCases, int cansPerCase )
      {
       int numberOfCans;

       numberOfCans = numberOfCases * cansPerCase;

       return numberOfCans;
      }

This is not a terribly complicated program but it can be analyzed. With careful observation, it can be noted that there are three lines of code in this function. Now the truth of the matter is that there could be a couple of dozen assembly/machine language statements involved in this function, but the analysis to be conducted is really comparing relative numbers of actions, so just counting the code lines is fine.

If another function uses a different algorithm to count cans and it takes seven lines of code, there is a reasonable chance that the other function will cause the program to run somewhat slower if this function is called frequently. The analysis give Computing Scientists apples to compare with other apples.

Monomial Analysis - Big O( N )

Now things get interesting when loops or other iterative activities get involved. Consider this code that counts the number of upper case 'A' letters in a list (i.e., an array).

   int findNumberOfAs( const int letterArray[], int arraySize )
      {
1      int index, aCounter = 0;

2      for( index = 0; index < arraySize; index++ )
          {
3          if( letterArray == 'A' )
              {
4              aCounter++;
              }
          }

5      return aCounter;
      }

This leads to a slightly more interesting analysis. Notice that a line number has been placed beside each line of code, and consider the following analysis.

• the code at line 1 will be implemented exactly one time. The two variables are initialized and nothing else needs to happen
• the code at line 2 will be implemented "arraySize" times, meaning since it will be iterated up to arraySize (or N as we will think of it), the line will go through the processor "arraySize" or N times
• the code at line 3 will also be implemented arraySize or N times; no matter what the outome of the if statement, it will go through the processor as many times as the for loop will
• the code at line 4 is hard to evaluate. Maybe the list is 50% 'A's or maybe it is just 5% 'A's. What is known is that the aCounter variable will be incremented some fraction of "arraySize" or N times, so for the short term, it is safe to say that it will iterate N/? times, with a rough guess being N/4
• finally, the code at line 5 is easy; the return statement will be implemented exactly once and the function will be over

Simple as this function is, it can be analyzed, and here is the analysis process:

• Add the counts from each line: 1 + N + N + N/4 + 1
• Combine the terms: (9/4)N + 2
• This puts the analysis in the monomial form C₁ * N + C₂ where the Cs are constant values
• The constants are removed, leaving N as the result
• The other action will be to identify the highest power of N which for purposes of this analysis is easy; it's N
• This is considered to have a time complexity of N, or Big O( N )

No part of this analysis process is difficult. One must simply keep track of all the code line actions of the operation, or in this case, the function.

Quadratic Analysis - Big O( N² )

Now consider the bubble sort from a previous section. The specification block and design comments are left out to keep it readable.

   void runBubbleSort_C( char letters[], int arraySize )
      {
1      int listIndex, swappingIndex;

2      for( listIndex = 0; listIndex < arraySize - 1; listIndex++ )
          {
3          for( swappingIndex = 0; 
                    swappingIndex < arraySize - 1; swappingIndex++ )
              {
4              if( letters[ swappingIndex ]
                                   > letters[ swappingIndex + 1 ] )
                  {
5                  swapCharsByIndex( letters,
                                 swappingIndex, swappingIndex + 1 );
                  }
              }
          }
      }

Hmmm. Nested loops. That will probably make a difference. Check out the analysis.

• Like the previous one, initializing the variables is just one step; nothing is repeated
• (Kinda) Like the previous one, the first or outer loop is iterating across the list, which of course would be N times. The fact that it iterates N - 1 times is not a concern since this whole analysis is an estimation
• Unlike the previous one, the second or inner loop also iterates N times. However, since it is iterating inside another loop that is iterating N times, this loop is actually iterating N² times
• The if statement, being inside the inner loop is also implemented N² times no matter what logical decision it makes
• And finally, the swap operation will be conducted an unknown number of times, however in a randomly sorted list, it is reasonable to estimate that the if statement will be true about half the time so it will be assumed that the swap operation will be implemented about N²/2 times. Again, remember that all the parts of this analysis are estimations

Repeating the analsysis process.

• add the counts from each line: 1 + N + N² + N² + N²/2
• Combine the terms in the quadratic form: (5/2)N² + N + 1
• This is in the quadratic form C₁N² + C₂N + C₃
• Remove the constants to leave N² + N
• Find the highest power of N, which is N² and remove the other one
• This is considered to have a time complexity of N², or Big O( N² )

Again, the analysis is straightforward, and Computing Scientists such as yourself can now conduct scientific analyses of sorting algorithms. Even when they do something weird as will be provided next.

Divide and Conquer - Big O ( Log₂ N )

There was another algorithm found in the previous sections that searched for data in a sorted list, the Binary Search alorithm. This one was unusual in that it eliminated half of the remaining search possibilities with every iteration, or recursive call. In other words, this strategy does not repeatedly iterate across the entire list even one time, let alone multiple times.

Since the code is a little more complicated for this, just consider the strategy:

1. Find the middle of the list and see if that item is the one being searched for
2. If it is not, find out where the search value is in the list: Is it higher than the middle item, or is it lower?
3. If the search value is higher than the middle of the list, stop searching the list below that value; it if search value is lower than the middle of the list, stop searching the list above that value
4. Either way, each pass will eliminate half the list (divide by roughly 2), making the binary search operation very effective, and very fast

Consider the following data related to the results of using this strategy

• It is found that if there are no more than 4 items in the list (i.e., N = 4), the maximum number of searches to find the value if it exists is 2
• It is found that if there are no more than 8 items in the list (i.e., N = 8), the maximum number of searches to find the value if it exists is 3
• It is found that if there are no more than 16 items in the list (i.e., N = 16), the maximum number of searches to find the value if it exists is 4
• It is found that if there are no more than 32 items in the list (i.e., N = 32), the maximum number of searches to find the value if it exists is 5
• It is found that if there are no more than 64 items in the list (i.e., N = 64), the maximum number of searches to find the value if it exists is 6

The astute Computer Scientist will note that the mathematical relationship here is:

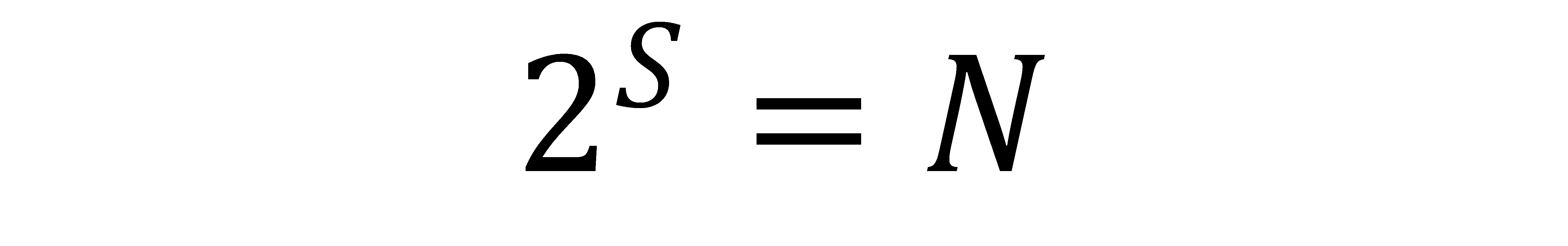
where S is the number of steps required to find a value and of course N is the number of values.

That's not a problem. From your math class, you know to take the log₂ of each side, as shown here.

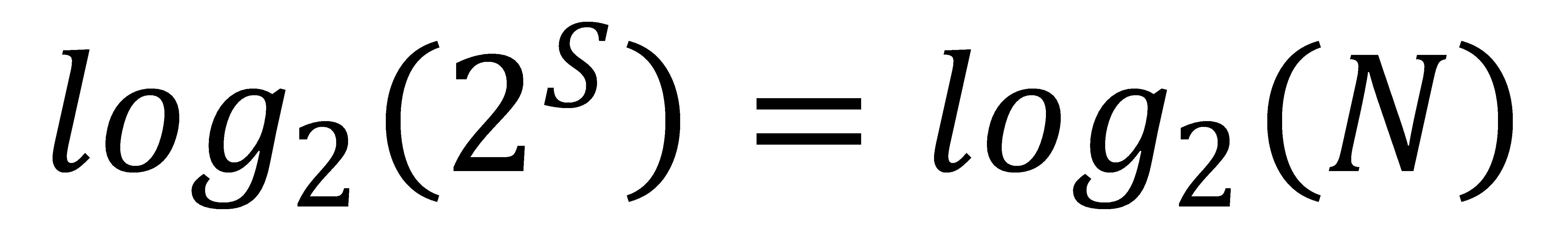
And then since the S can be brought in front of the left log₂ leaving log₂ of 2, and that is one, the result for finding the number of steps for this search is shown here.

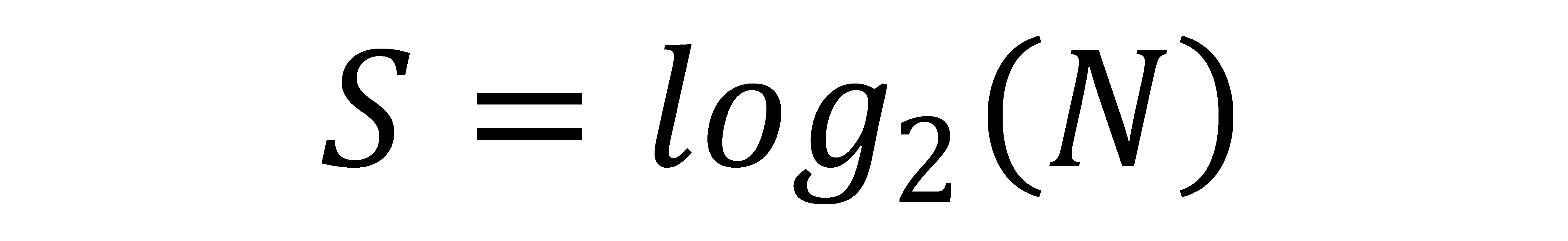
The number of steps required to search for an item is the log base two of N. Think about that.

And then expand your thinking. The number of steps for the binary search of 1,000 items would be 10, the number of steps for the binary search of 100,000 items would be 17, and the number of steps for the binary search of 1,000,000 would be 20.

An N² search of 1,000,000 would require 1,000,000,000,000 (1 trillion) operations. It should be pretty obvious why Computing Scientists like to study this stuff.

Complexity/Big O Analysis

This chapter initiates learning on time complexity, or the analysis of how much time an operation might take. The analysis is conducted in such a way that differing algorithms may be compared to each other. From the text, it is pretty obvious that this kind of analysis is a rough estimate but it can be very helpful when deciding which algorithm might be used for a given operation.

There will be a brief discussion of complexity/Big O analysis in the advanced sorting chapter but this section provides the foundation needed to understand the process and successfully apply it.

One extra note here at the end. There is a web site called BigOCheatSheet that covers all of what is found here and quite a bit more. It is worth your time to check it out.